Data Mining (78 page)
Authors: Mehmed Kantardzic

We can see that after the first iteration, the total square-error is significantly reduced (from the value 27.48 to 6.17). In this simple example, the first iteration was at the same time the final one because if we analyze the distances between the new centroids and the samples, the latter will all be assigned to the same clusters. There is no reassignment and therefore the algorithm halts.
In summary, the K-means algorithm and its equivalent in an artificial neural networks domain—the Kohonen net—have been applied for clustering on large data sets. The reasons behind the popularity of the K-means algorithm are as follows:
1.
Its time complexity is O(n × k × l), where n is the number of samples, k is the number of clusters, and l is the number of iterations taken by the algorithm to converge. Typically, k and l are fixed in advance and so the algorithm has linear time complexity in the size of the data set.
2.
Its space complexity is O(k + n), and if it is possible to store all the data in the primary memory, access time to all elements is very fast and the algorithm is very efficient.
3.
It is an order-independent algorithm. For a given initial distribution of clusters, it generates the same partition of the data at the end of the partitioning process irrespective of the order in which the samples are presented to the algorithm.
A big frustration in using iterative partitional-clustering programs is the lack of guidelines available for choosing K-number of clusters apart from the ambiguity about the best direction for initial partition, updating the partition, adjusting the number of clusters, and the stopping criterion. The K-means algorithm is very sensitive to noise and outlier data points, because a small number of such data can substantially influence the mean value. Unlike the K-means, the
K-mediods
method, instead of taking the mean value of the samples, uses the most centrally located object (mediods) in a cluster to be the cluster representative. Because of this, the K-mediods method is less sensitive to noise and outliers.
Fuzzy c-means
, proposed by Dunn and later improved, is an extension of K-means algorithm where each data point can be a member of multiple clusters with a membership value expressed through fuzzy sets. Despite its drawbacks, k-means remains the most widely used partitional clustering algorithm in practice. The algorithm is simple, easily understandable and reasonably scalable, and can be easily modified to deal with streaming data.
9.5 INCREMENTAL CLUSTERING
There are more and more applications where it is necessary to cluster a large collection of data. The definition of “large” has varied with changes in technology. In the 1960s, “large” meant several-thousand samples for clustering. Now, there are applications where millions of samples of high dimensionality have to be clustered. The algorithms discussed above work on large data sets, where it is possible to accommodate the entire data set in the main memory. However, there are applications where the entire data set cannot be stored in the main memory because of its size. There are currently three possible approaches to solve this problem:
1.
The data set can be stored in a secondary memory and subsets of this data are clustered independently, followed by a merging step to yield a clustering of the entire set. We call this approach the divide-and-conquer approach.
2.
An incremental-clustering algorithm can be employed. Here, data are stored in the secondary memory and data items are transferred to the main memory one at a time for clustering. Only the cluster representations are stored permanently in the main memory to alleviate space limitations.
3.
A parallel implementation of a clustering algorithm may be used where the advantages of parallel computers increase the efficiency of the divide-and-conquer approach.
An incremental-clustering approach is most popular, and we will explain its basic principles. The following are the global steps of the incremental-clustering algorithm.
1.
Assign the first data item to the first cluster.
2.
Consider the next data item. Either assign this item to one of the existing clusters or assign it to a new cluster. This assignment is done based on some criterion, for example, the distance between the new item and the existing cluster centroids. In that case, after every addition of a new item to an existing cluster, recompute a new value for the centroid.
3.
Repeat step 2 until all the data samples are clustered.
The space requirements of the incremental algorithm are very small, necessary only for the centroids of the clusters. Typically, these algorithms are non-iterative and therefore their time requirements are also small. But, even if we introduce iterations into the incremental-clustering algorithm, computational complexity and corresponding time requirements do not increase significantly. On the other hand, there is one obvious weakness of incremental algorithms that we have to be aware of. Most incremental algorithms do not satisfy one of the most important characteristics of a clustering process: order-independence. An algorithm is order-independent if it generates the same partition for any order in which the data set is presented. Incremental algorithms are very sensitive to the order of samples, and for different orders they generate totally different partitions.
Let us analyze the incremental-clustering algorithm with the sample set given in Figure
9.6
. Suppose that the order of samples is x
1
, x
2
, x
3
, x
4
, x
5
and the threshold level of similarity between clusters is δ = 3.
1.
The first sample x
1
will become the first cluster C
1
= {x
1
}. The coordinates of x
1
will be the coordinates of the centroid M
1
= {0, 2}.
2.
Start analysis of the other samples.
(a)
Second sample x
2
is compared with M
1
, and the distance d is determined
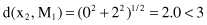
Therefore, x
2
belongs to the cluster C
1
. The new centroid will be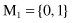
(b)
The third sample x
3
is compared with the centroid M
1
(still the only centroid):
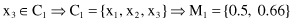
(c)
The fourth sample x
4
is compared with the centroid M
1
:
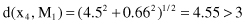
Because the distance of the sample from the given centroid M
1
is larger than the threshold value δ, this sample will create its own cluster C
2
= {x
4
} with the corresponding centroid M
2
= {5, 0}.
(d)
The fifth sample x
5
is compared with both cluster centroids:
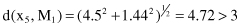
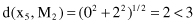
The sample is closer to the centroid M
2
, and its distance is less than the threshold value δ. Therefore, sample x
5
is added to the second cluster C
2
:
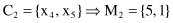
3.
All samples are analyzed and a final clustering solution of two clusters is obtained: