Mathematics and the Real World (16 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

During many years of activity, Galileo was supported by many different groups, including the Church, but a combination of internal politics and ideology resulted in the Inquisition demanding that Galileo destroy his books and renounce his theory. His famous trial ended with his being sentenced to imprisonment, which was then changed to house arrest. In his trial he retracted his support of Copernicus. Years later the story spread that at the end of the trial he muttered to himself, “and yet it does move” (i.e., the Earth does move around the Sun).
The opposition of the Church to Galileo's discoveries was supported by, and some would say initiated by, the most prominent and influential scientists and philosophers of the time, who adhered to, taught, and believed in Aristotle's theory. They also rejected Galileo's actual discoveries. They claimed, for example, that what appeared to be the moons of Jupiter and the phases of Venus resulted from the use of lenses and did not exist in reality. They proved this by noting that what seemed to be the moons of Jupiter and the phases of Venus disappeared without the use of a telescope. Today their claim seems absurd. Lenses are used to enable us to see better. We must bear in mind, however, that the telescope itself, how it works, and its capabilities were then new and unknown to scientists. In a like manner, those philosophers did not accept the existence of the mountains
that Galileo discovered on the Moon and explained that what seemed to be mountains on the Moon was a reflection of the mountains on Earth in a crystalline substance surrounding the Moon. Opposition of this kind continued throughout the years of Galileo's activity.
Galileo's main contribution to astronomy was in the field of observation; he did not contribute much in the area of theory. For the same reasons that guided astronomers from the time of the Greeks to Copernicus, Galileo accepted the assumption that celestial bodies moved in perfect circles and therefore vigorously opposed Kepler's model of elliptical orbits. At that time it was still believed that the laws of movement of celestial bodies were different than the laws of movement on Earth. Galileo therefore saw no discrepancy between the assumption that the stars moved in perfect circles and the actual movement of objects on Earth, which sometimes appears tortuous or crooked. The strictly controlled experiments that Galileo conducted on the movement of objects, and specifically on falling bodies, together with the mathematical explanations he used to describe that movement, constituted an essential element on which Newton's findings were based, but it was only as a result of Newton's findings that movement on Earth and that of heavenly bodies were first consolidated into one system. Galileo Galilei and the British philosopher Francis Bacon (1561–1626) were the principal formulators of the empirical method in modern science. The empirical method advocates learning from controlled experiments both to make new discoveries and to check, confirm, or refute scientific theories. This was a sharp deviation from the hitherto accepted episteme, or system of scientific knowledge, formulated by the Greeks that was apprehensive about biases and illusions inherent in observations, which they thought were likely to lead to incorrect theories.
The experiments that Galileo performed with moving and falling bodies were not innovative. Similar experiments had been carried out by others before him to discover the rules of the motion of bodies. Prominent among those earlier experimenters was the mathematician Niccolò Tartaglia (1499–1557), whose influence is mentioned in Galileo's writings; we will discuss some of his other contributions further on. The special element in Galileo's work was the almost-modern combination
of theoretical mathematical arguments, which were then corroborated by experiments, and experiments that led to hypotheses about mathematical laws of nature. He dropped objects from the top of a tower (apparently the Leaning Tower of Pisa, although there is no clear-cut evidence of this) and found that the speed at which a body falls in a vacuum does not depend on its weight. In his first reports Galileo stated that the speed at which a heavy body falls is only slightly different from that of a lighter body, and he used that to show that Plato and Aristotle's theory that the speed at which a body falls is determined by its weight is not correct. Later, Galileo discovered that the differences in the speed of falling bodies in his original experiments were due to friction with air and that in a vacuum there is no difference in the speed at which the bodies fall. Experiments Galileo performed of rolling balls down a slope and measurements he took of the trajectories of stones projected parallel with the ground led him to conclude that one can distinguish between the movement in the accelerated fall of a dropped object and movement in a straight line. He also showed the numerical link he found between uniform motion and accelerated motion, such as:
| | Progress in time | 1, 2, 3, 4,… |
| | Progress in distance | 1, 4, 6, 16,… |
In other words, the distance is proportional to the square of the time. This relation between the numbers and their squares led Galileo to consider the concept of infinity, as we will see in section 59. The law of motion that Galileo derived from these measurements prevented him from discovering the general rule. He noted that the differences between the distances covered by a body between two equal and consecutive periods of time increase like the odd numbers, 3, 5, 7, 9,…Indeed, the equation (
n
+ 1)
2
–
n
2
= 2
n
+ 1 proves easily that the differences between the squares of the integers are the odd numbers. Galileo thought it right to consider specifically the ordered manner of these differences as a law of nature. Thus he continued the Pythagorean tradition that explains nature via the relation between numbers. His experiments with a ball rolling down a slope confirmed these theoretical claims (the numerical confirmation was so exact
that later researchers accused him of tampering with the empirical results to make them conform to the theory).
Galileo also found that the geometrical path of a ball thrown parallel with the ground is a parabola, a curve well known to the Greeks that had been studied in depth by Apollonius. The link with mathematics, in particular the fact that a parabola is the function that describes motion, was emphasized by Galileo. He also put forward an early version of the law of inertia, which states that in the absence of a force acting upon it, a body in motion will continue at the same uniform speed. Galileo thus repudiated Aristotle's approach that a force was required to start and maintain motion. Together with his empirical findings in astronomy and in the study of motion, Galileo's enormous contribution to the connection between science and mathematics—a contribution that served as a basis for Newton's laws—was his method of using observations to derive the relation between different elements such as time, speed, and acceleration. These precise mathematical connections, or functions, served Newton in his own research.
René Descartes disagreed with laws of nature in the form of the formulae proposed by Galileo. His objection was that they were derived from experiments and not from underlying physical principles. In this sense, Descartes was following the Aristotelian tradition. Descartes was born in 1596 to a wealthy family in La Haye, in the Loire valley in France. The town was later renamed Descartes. His family's prosperity meant that he was spared financial concerns throughout his life. A valet accompanied him wherever he went, even when Descartes volunteered as a soldier in the army of Duke Maximilian of Bavaria. This act reflects the spirit of adventure and wanderlust of the young Descartes, whose travels took him all over Europe. In Holland he met the mathematician Isaac Beeckman, who held fruitful discussions with him on philosophy and mathematics and who put to him mathematical questions that spurred his interest in mathematics and physics. Descartes spent many years in Holland but left suddenly to return to France to manage the family's affairs. In the same spirit of restiveness, he accepted an invitation from Queen Christina of Sweden to become her tutor and
the chief scientist of her country. He became ill soon after arriving in Sweden and died in 1650.
Descartes's major contribution was in general philosophy. He is considered to be the father of modern philosophy, but we will not expand on that here. We will observe just that he tried to extend the logical approach to encompass all facets of life. He coined his famous saying “
Cogito, ergo sum
” (“I think, therefore I am”) as a building block in the structure of logic used to reach philosophical statements. He realized that our senses indicate physical truths, like the sun rises, blood flows, and so on. But without the use of our mind, these “truths” do not make sense. He also claimed that the senses may fool us, hence we have to doubt every observation and check and recheck any logical step and conclusion that we arrive at. We have already stated that urging people to be constantly skeptical is urging them to behave in a way that is opposed to human nature, opposed to what evolution has prepared us for.
Descartes bequeathed to mathematics the consolidation of algebra and geometry. Since Eudoxus in classical Greece, algebra and geometry developed along parallel paths with very few meeting points. Algebra dealt with numbers and attempts to find numerical solutions to algebraic equations. A simple example that we encounter in school is seeking the solutions to the equation 2
x
+ 5
y
= 8, or the equation
x
2
+
y
2
= 9. Geometry tried to find the relation between various geometric shapes and their properties. Descartes demonstrated that geometric shapes can be described by algebraic equations. For instance, the solutions to the first equation we put down is a straight line in the (
x
,
y
)-plane, while the solutions to the second equation form a circle of radius 3. Descartes's contributions were not stated in the modern terms of a plane and its coordinates. An algebraic representation of a plane and its coordinates had not been created yet. But his ideas have led to the development of the system of coordinates for planes and spaces that we know today. The system of Cartesian coordinates taught today in all schools is a development based on Descartes's approach, and it is therefore named after him (his Latin name, which he used in many of his writings, was Renatus Cartesius). This mathematical tool enabled Newton to develop a new mathematics and formulate with it the laws of nature, as we will see later.
17. ELLIPSES VERSUS CIRCLES
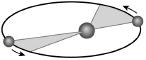
An important step in presenting a picture of the world as we know it was made by Johannes Kepler. We will first state Kepler's three laws of planetary motion, which constitute his main contribution to the mathematical description of the world. We will then review the tortuous path by which he reached these understandings.
Kepler's first law
: The path of the planets about the Sun is elliptical in shape, with the Sun being located at one focus of the ellipse.
Kepler's second law
: The speed of each planet on its orbit is such that the line from its location on the ellipse to the Sun covers equal areas in equal periods of time.
Kepler's third law
: The square of the time taken by a planet for a complete orbit around the Sun is proportional to the cube of its average distance from the Sun. This can be written as
T
2
= kD
3
,
where
T
is the time of the planet to complete one round,
D
is the average distance of the planet from the Sun, and
k
is the same constant for all planets.
It is hard to overstate the mental difficulties Kepler overcame in presenting his three laws, and in particular the first one. The first law was formulated in accordance with the classical Greek approach describing the world with the help of geometry. At a remove of four hundred years, the transition from a circle to an ellipse seems simple. Today we actually consider a circle as a special instance of an ellipse in which the two foci converge. Kepler's first law, however, represented a contradiction to the deep-rooted
tradition of two thousand years that as the firmament is perfect, the orbits of the planets must be perfect and, hence, circular. Kepler changed circles for ellipses and did not offer a reason or alternative purpose. His law was based on observations and measurements. At that time, those observations did not constitute clear proof of his claim, as the ellipses along which the planets moved were very close to circles, and the means for measurement in those days made it very difficult to differentiate between them. Kepler's ellipses did however enable the use of epicycles revolving around deferents to be abandoned, thereby offering a great simplification of the system.