Mathematics and the Real World (14 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Aristotle based the principles of his theory on observations from nature. For example, he said, human beings grow teeth, the purpose of which is to chew food. Rain falls (or in Aristotle's words, the gods bring down rain), the purpose of which is to make grains grow, and similarly with other laws of nature. The purpose of the events that we see in nature enables us to discover the laws underlying the events, and vice versa, the purpose that we discover by virtue of our intelligence enables us to forecast those events. From a retrospective view it can be seen that although the cause and effect for Aristotle were totally different than those derived from the laws of
evolution, the structure of Aristotelian thought is very similar to viewing nature via the evolutionary process. For Aristotle, the growth of teeth was a law of nature, and its purpose was to enable living beings to eat, while the evolutionary standpoint states that those living beings that grew teeth, enabling them to chew food, were the ones that developed. Likewise, Aristotle claimed that rain was a law of nature whose purpose was to enable grains to grow, whereas viewed from the evolutionary standpoint, grains developed in areas where there was rain. Either of these approaches helps us learn from the characteristics that we can observe how things developed. And vice versa, from the purpose, according to Aristotle, or from the conditions, according to evolution, we can predict the characteristics that we can see in nature.
Aristotle also expressed his views on the essence of space and motion in space. He saw bodies that fell to the ground, while other materials, such as flames or steam, rose. Whereas Plato tried to explain this by relating to the different weights of the various entities, Aristotle concluded that the purpose of pristine, pure elements such as steam or fire was to reach heaven, a pristine, pure place, while the purpose of materials such as ash or soil, which are clearly impure, was to reach the ground. His view was supported by the belief that the angels and gods, which are pure by definition, dwell in heaven. This led Aristotle to define a space that has directions, up and down. Upward is the direction toward the pure and the good, while downward is the spoiled and defective, toward the center of the Earth (even today,
upward
represents positive progress and
downward
signifies regression). This view of space answered the question about the antipodes, or specifically, what do up and down mean for people on opposite sides of the Earth.
Downward
for those on the other side of the Earth also means toward the center of the Earth, said Aristotle, hence they are not standing on their heads. This geometric view of the Earth as a sphere is of course consistent with ours. The purpose underlying Aristotle's directions up and down, relative to the Earth, firmly established the Earth as the center of the world for many years and predominated over other models, which in due course proved to be more correct.
With regard to the movement of various bodies, both earthly and heavenly,
Aristotle observed that heavenly bodies moved in smooth, regular paths, a straight line or a circle, while earthly bodies moved along much more tortuous routes. The purpose that considered upward to represent purity while downward indicated inferiority led him to conclude that circular and straight paths were pure and other routes were defective. As it was geometry that served to describe the movement of the various bodies, Aristotle reasoned that the movements of heavenly bodies and earthly bodies were governed by different sets of rules. The gap between the different descriptions of earthly and heavenly motion persisted until the seventeenth century, when it was bridged by Newton. Aristotle also searched for a reason for the motion of the different bodies, and, by implication from the perception that the force exerted on a body causes it to move, he concluded that a force is responsible for all motion. Aristotle applied this conclusion to the heavenly bodies also. Hence, he claimed, the stars cannot move in a vacuum, and the world is filled with a substance he called
ether
. The ether also explained the source of the light and warmth of the Sun. The friction between the Sun and the ether creates heat. Aristotle went beyond that and rejected the model that described the world as consisting of atoms with a vacuum between them, as that would not allow for the exertion of the force required for motion. Hence, matter is continuous. The model of the atoms and the rejection of the assumption of the existence of the ether held until the nineteenth and twentieth centuries. Although many of the conclusions drawn from Aristotle's philosophy slowed the development of science, his philosophical principles nevertheless made an important contribution to scientific development.
14. MODELS OF THE HEAVENLY BODIES (CONT.)
Aristarchus of Samos (310–230 BCE) made a radical proposition about the motion of the heavenly bodies. He claimed that it was not the Earth but the Sun that was at the center of the universe and that the Earth and the other planets orbited the Sun. We know of the activity of Aristarchus from one essay that has survived in its entirety, in which he calculated the sizes of
various astronomical bodies and distances, including the size of the Earth and the Sun, and the distance of the Earth from the Sun and the Moon. Archimedes, with whom Aristarchus was in contact, refers in his writings to the doctrine of Aristarchus. Aristarchus developed methods for calculating and measuring that resulted in assessments that were very advanced for their time but are very different from the facts as we know them today. For example, he assessed that the ratio of the distance of the Moon from the Earth to the distance of the Sun from the Earth was 1 to 19, whereas the correct ratio is 1 to 380. These and other measurements resulted in his proposing a heliocentric model (i.e., with the Sun at the center). The reason he gave was aestheticism. It was unreasonable to think that such a large body as the Sun would revolve around such a relatively small Earth. Aristarchus, who was affected by the views of the Pythagoreans, thought that the Sun was the fire at the center of the universe. He also realized that Eudoxus's model of spheres and its later developments can be more easily explained if it is assumed that the planets orbit the Sun and that the Earth also revolves on a circular path around it.
Although Aristarchus's model was widely known by the Greek astronomers, it was not generally accepted by them. There were several reasons for its rejection, some philosophical, and some scientific. The philosophical argument was the almost religious Aristotelian claim regarding the purity of the heavens as opposed to the impurity of Earth. One report states that Aristarchus himself was accused of heresy regarding those religious principles, but such accusations were not characteristic of the Greek environment that permitted pluralism of expression. The scientific objections to Aristarchus's model, however, were serious. One was that if the Earth moved around the Sun, then from different locations on its orbit the angles between the stars would be different, and that was not the case. This reason was quoted by Aristotle himself as an argument against the possibility that the Earth revolved around the Sun. It was not until many years later that the different angles between how we see the stars were revealed, differences that were too small for the Greeks to measure. Another argument against the centrality of the Sun was that if the Earth orbited the Sun, its speed would have to be so great that anything on the surface of the Earth
would be propelled off it into space. We will address this claim when we discuss Ptolemy.
Further crucial progress in the calculation of cosmological data was made by Erastothenes (276–195 BCE). He was born in Cyrene, in what is today Libya, and carried out most of his scientific work in Alexandria, Egypt. He held the distinguished role of chief librarian of the widely known Great Library of Alexandria. Today's students know the name Erastothenes because of the “Sieve of Erastothenes,” an (inefficient) way of finding all the prime numbers. He took it upon himself to calculate the dimensions of the Earth. He noticed that at noon, in the city of Syene (known today as Aswan), an upright pole does not cast a shadow, whereas at the same time in Alexandria, it does. By measuring the angle of the shadow in Alexandria and the distance between the two cities, which lie on the same longitude, he managed to estimate the dimensions of the Earth. The methods used by Aristarchus, Erastothenes, and their colleagues to perform their calculations are themselves very interesting, but beyond that, they provide evidence of the progress of practical mathematics in Greece, mathematics that served the Greek engineers and builders, who made remarkable achievements. Greek mathematics, fed by Egyptian and Babylonian ideas and achievements, constituted significant further development. Archimedes of Syracuse (287–212 BCE) was perhaps the best-known mathematician of that period for his mathematics-based engineering developments. We will allude to his contribution later.
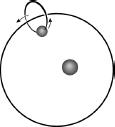
Two far-reaching proposals regarding the model of the motion of celestial bodies were made by Apollonius of Perga (262–190 BCE). One was that the center of the circle on which a planet moved was not necessarily the center of the Earth. The other was that a planet can revolve along a perfect circle around a point that is itself revolving along a perfect circle around the Earth. He arrived at these views through his research into curves in a plane, particularly those created by orbiting in a small circle, known as an epicycle, the center of which moves along a larger circle, which the Greeks called a deferent. The curve thus created orbits around the deferent in a way very similar to the way the Moon revolves around the Sun. This motion is made up of two paths that sometimes move in opposite directions. Hence
the motion is not constant but is sometimes forward and sometimes backward. This irregularity, combining progression and regression, is in some way similar to the irregularity of the paths of the planets, and Apollonius therefore proposed that the epicycles around the deferent were the paths of the planets. (See the diagram below, showing the Earth not at the center of the circle and the movement of the planet along the epicycle.) These two amendments to the previously held views enabled Apollonius, of course, after detailed calculations, to present a mathematical system of planetary motion that fitted well with the facts known at that time.
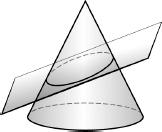
It is interesting that Apollonius, who is known for his contribution to geometry in general and who also carried out rigorous research into the properties of lines in a plane and the structure of three-dimensional bodies, was very familiar with ellipses. One of his better-known studies dealt with the structure of cones and the shape of their two-dimensional cross-sections. His research showed, for example, that the shape formed by a two-dimensional plane that intersects a cone could be a parabola, a hyperbola, or an ellipse (see the diagram below). Yet, although he was familiar with the shape of an ellipse, it did not occur to him to suggest that the paths followed by the planets were in fact ellipses. It took another fifteen hundred years to reach this conclusion.
Hipparchus (190–120 BCE) took the mathematics of the model of the motion of celestial bodies to another level. Most of what we know of Hipparchus comes from the writings of Ptolemy, who called him the greatest Greek astronomer. Hipparchus did most of his scientific work on the island of Rhodes. Thirty-five years of astronomical observations that Hipparchus carried out on Rhodes combined with astronomical data from the Babylonians resulted in his constructing an astronomical model with previously unknown precision. For example, following his studies, the Greeks could forecast an eclipse of the Moon with an accuracy of within one hour. Hipparchus also discovered and measured the precession of the equinox (which we now know is caused by the movement of the plane of the Earth's orbit with regard to the position of the stars) and calculated the length of the cycle of this movement (about 2,600 years). His measurements greatly improved the data on the sizes of the heavenly bodies, the Sun, and the Moon, as well as their distance from the Earth, and data on the seasons, the times of the equinox, and so on. Hipparchus's major mathematical contribution was in the development of trigonometry. He defined trigonometric values, such as the sine and tangent of an angle, and found basic relations between them that helped him in his calculations. Following these definitions, he himself and his contemporaries constructed tables of what is today called the sine function (see the diagram), that is, the graph of the sine of every angle (the ratio of the line opposite the angle in a right triangle to the length of the hypotenuse), as well as other trigonometric functions, such as cosine and tangent. These functions fulfilled a major role in describing nature from the time of the Greeks to today.