My Time in Space (21 page)
Authors: Tim Robinson

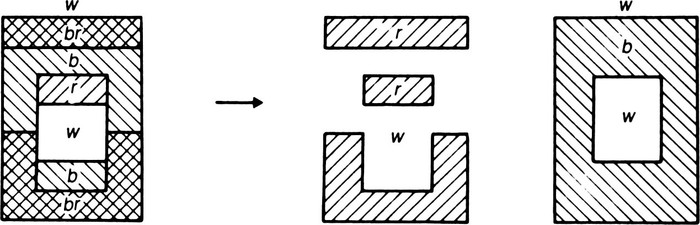
Fig. 20. A four-coloured map and its two-coloured factors.
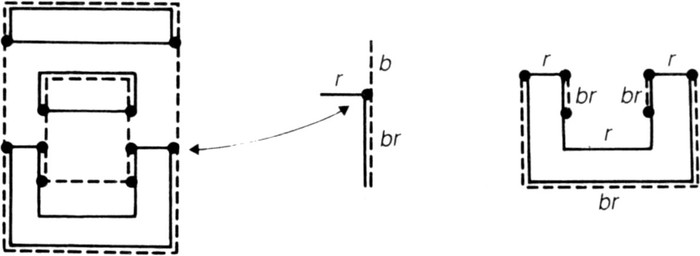
Fig. 21. The three types of border in a four-coloured map, and the alternation of types of borders around one of its regions.

Fig. 22. A symmetrical map (derived from a regular solid, the dodecahedron), colourable with some puzzling, and the petersen, an uncolourable network.
Without going too far into the lengthy reasoning necessary to capture this proof, I can give the willing reader a glimpse of the striking techniques for manipulating the colourings of maps that Spencer-Brown has devised on the basis of the above simple ideas. First we shift attention from the regions of the map to its network of borders. Fig. 21 shows how the borders of the four-coloured map shown in Fig. 20 are made up from the borders of its two
factors
. Note that at each node borders of three types meet. We can think of them as having three different colours. A little
experimentation
will convince the reader of the theorem (first published by P.G. Tait in 1880) that if a map can be four-coloured, its network of borders can be three-coloured (i.e. coloured so that the three borders meeting at a node are all of different colours), and vice-versa. So the problem of four-colouring maps has been reduced to one of three-colouring (standard) networks. Just to show that this is a real problem, here are two little labyrinths, in one of which lurks the beast, uncolourability (Fig. 22). By trial and error the ingenious reader will be able to colour the first, but the other, a fascinating entity known as the petersen, cannot be three-coloured; in fact it is the smallest of all the uncolourable
networks. It is three-dimensional, and since its links pass under and over each other they cannot be the borders of regions in a map; so it is not a counter-example to the four-colour map
theorem
. (One of Spencer-Brown’s proofs of the theorem proceeds by showing that all uncolourable networks must be three-
dimensional
, from which it would follow that all planar networks are colourable.) It is instructive to try colouring the petersen, starting from any node and working outwards, labelling the links 1, 2 or 3, adhering to the rule that the three links meeting at any node must have different labels. Whatever choices one makes in this process, one soon finds oneself trapped in a corner where one cannot avoid breaking the rule. The sensation is like that of
coming
up against a contradiction in a chain of reasoning, or of trying to work out whether the statement ‘This statement is false’ is true or false. Paradoxicity, not uncolourability, is the relevant paradigm in this mathematical situation, according to Spencer-Brown; the network
is
colourable – but only with imaginary colours
analogous
to the imaginary values he introduces as solutions of
self-contradictory
equations in
Laws
of
Form.
(This is the great leap from
Laws
of
Form
to the four-colour theorem that I jibbed at, in that last apocalyptic telephone conversation.)
I shall try to convey the fascination and simplicity of
Spencer-Brown’s
methods and follow him some way into the theory of map colourations. Returning to Fig. 21, we can take the three colours of the network to be blue, red, and blue-red, i.e. purple (
b,
r
, and
br
). Of course at this stage we do not know if all maps can be four-coloured, or, equivalently, if all planar networks can be three-coloured; so we have to be able to represent a link we cannot colour or which we choose to leave uncoloured.
Fortunately
we have the fourth alternative in Spencer-Brown’s logical
pattern, neither
b
nor
r
, for such a link. Note that the links
involving
r
, for instance, form closed circuits, around which they
alternate
:
r
,
br,
r
,
br
etc. (These circuits are just the boundaries of the colour-patches in the
r
-factor of the map.) Suppose we have
succeeded
in three-colouring a network in which there is a circuit as shown in Fig. 23. Clearly we can interchange the
b
-links with the
br
-links without having to change any of the
r
-links and so
upsetting
the colouration of the rest of the map. This is the sort of operation one often needs to perform in map-theory, and Spencer-Brown has invented a brilliant way of thinking about it. Imagine one could take a closed band of colour
r
and superimpose it on the circuit. What are the rules for superimposing one colour on another? (Instead of ‘superimpose’ we should say ‘idempose’, as the two colours will not just be one on top of the other but will occupy the identical space.) The answer goes to the heart of what Spencer-Brown calls ‘formal mathematics’, that is, the
mathematics
of elements whose order, size and shape are undefined or
irrelevant
. Consider a region in a map, and another region of the same colour idemposed on the map so that part of its border coincides with part of the border of the first region (Fig. 24). Since we have the same colour on either side of it, we can omit the doubled part of the border; the two regions fuse like raindrops, eliminating the surface films between them. This suggests that the rule should be that idemposition of two identical elements cancels both of them:
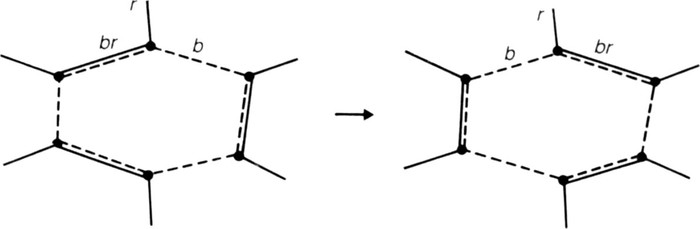
Fig. 23. Interchanging the two types of border round a circuit.

Fig. 24. Eliminating borders between two regions of the same colour. (For
clarity
the two borders are shown slightly separated where they in fact coincide.)
rr
= .
(Of course real colours do not behave in this way; we have to idealize them somewhat in order to use them in the
representation
of abstract, formal, elements.) This ‘Axiom of Idemposition’ relates profoundly to
Laws
of
Form.
Fig. 24 is analogous to one of the primitive equations of the arithmetic of indications,
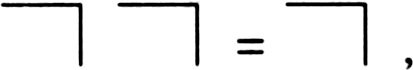
and if one of the regions totally surrounds the other the two
borders
cancel each other completely, which gives us the other
primitive
equation,
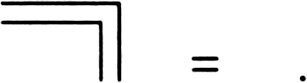
It follows that if we idempose a band of colour
r
on a circuit made up of alternating links
b,
br,
b,
br,
etc., all the
b
-links will become
br
-links and all the
br
-links will become
b
-links, since
brr = b.
This is exactly the operation shown in Fig. 23.
I will take this exposition just one step further. A typical
situation
in network-colouration arises when all the links have been coloured except one. Suppose the uncoloured link spans a circuit of alternating
b-
inks and
br-
links,
as in Fig. 25. As things stand we cannot colour it in correctly because there would then be nodes at either end of it in which two identically coloured links meet. But if we run an
r
-band around the closed path made by the uncoloured link and either the left-hand or the right-hand half of the original circuit, all is well; the missing link is now coloured
r
, and the links joining it at top and bottom are
b
and
br
. Since none of the links connecting this circuit to the rest of the network have been changed, we have coloured in the last link without upsetting the rest of the colouration.