My Time in Space (18 page)
Authors: Tim Robinson

where the string of dots indicated that the same pattern continues indefinitely. We can write this as

and say that
f
is re-entered into itself. Equations of this sort can have two solutions; for instance
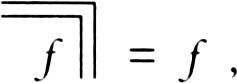
whether
f
= 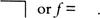
An obstacle, i.e. a spur to invention, then arises:
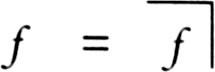
does not work for either of the standard values of
f
. Whatever the value of
f
, the equation contradicts itself; it has the structure of a paradox. Spencer-Brown proposes to call the value of
f
imaginary in such cases. (Analogously, in the algebra of numbers, when we come to an equation like -1/x = x,
which is not satisfied by any real number, we invent the so-called ‘imaginary’ number
i,
defined as a solution of that equation. It is routine in both pure and applied mathematics to use such imaginary numbers in
calculating
results represented by real numbers.) Or we can imagine a tunnel undermining the distinction which up to now has been inviolate (Fig. 18), and picture the value of
f
flowing outwards, changing from ‘marked’ to ‘unmarked’ or vice versa as it crosses the boundary, and re-entering through the tunnel. The value at any fixed point P would then flip between ‘marked’ and ‘unmarked’ continually as if a train of square waves were passing it.
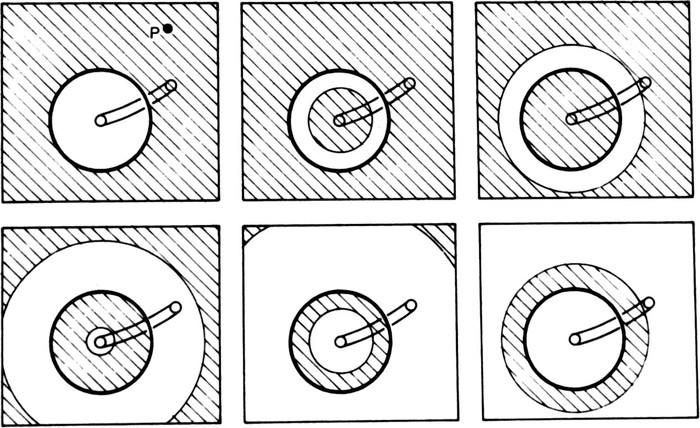
Fig. 18. An undermined distinction, and successive stages in the outward
propagation
of a value and its re-entry through the tunnel.
This introduction of time permits the use of the calculus in the design of switching circuits, and the main text ends with a
diagram
of an arrangement that flips from one value to the other every second time a variable within it flips; i.e. it is a counting device, and it has practical applications, being ‘the first use, in a switching circuit, of imaginary Boolean values in the course of the construction of a real answer’. Finally, in two appendices
Spencer-Brown
uses his calculus to prove the axioms of Boolean logic, and gives it an interpretation by identifying the marked state with ‘true’ and the blank space or unmarked state with ‘false’.
This extraordinary construction (epoch-making, indeed, if it accomplishes what it claims to have done) was written in a style of Pascalian grace, if not with irreproachable clarity; its air of stark rigour contrasted strangely with the somewhat shamanistic view of the mathematician it implied, as the one who brought back almost incommunicable truths from a distant and dangerous Otherworld:
To any person prepared to enter with respect into the realm of his great and universal ignorance, the secrets of being will eventually unfold, and they will do so in a measure according to his freedom from natural and indoctrinated shame in his respect of their revelation.
To arrive at the simplest truth … requires
years
of
contemplation.
Not activity. Not reasoning. Not calculating. Not busy behaviour of any kind…. Simply
bearing
in
mind
what it is one needs to know. And yet those with the courage to tread this path to real discovery are not only offered practically no guidance on how to do so, they are actively
discouraged
and have to set about it in secret, pretending meanwhile to be
engaged in the frantic diversions and to conform with the deadening
personal
opinions which are being continually thrust upon them. In these circumstances the discoveries that any person is able to undertake
represent
the places where, in the face of induced psychosis, he has, by his own faltering and unaided efforts, returned to sanity. Painfully, and even dangerously, maybe. But nonetheless returned, however furtively.
What appealed to my temperament most deeply in
Laws
of
Form
was its conceptual knife-play. ‘The theme of this book is that a universe comes into existence when a space is severed or taken apart,’ says Spencer-Brown in an introductory note. As a
beginning
, this move has its precedent: ‘The earth was without form, and void…. and God said, Let there be light: and there was light … and God divided the light from the darkness.’ That the basis of existence is difference, that the first step in understanding is
discrimination
, is for me an axiom that feels as if it were innate. As it happened, while I was dealing with Spencer-Brown’s diagrams I was also writing a catalogue note for an exhibition of abstract paintings by my closest friend, Peter Joseph, and I borrowed Spencer-Brown’s dictum as an epigraph:
‘…
a
universe
comes
into
being
when
a
space
is
severed
…’
… a world in which the divisions of night from day, the shores, the
horizons
, are sharp enough to cut you. In the paintings of ’67–8 Peter Joseph reduces landscape to the clearest oppositions of the simplest elements, each work being composed of just three or four rectangles of pure colour…. One of these paintings, a long rectangle divided once from top to bottom and once from side to side to give four identical areas,
conveys
the sensations one would hope for from a trans-polar orbiting: three of its quadrants, in brilliant but somehow sombre primaries, have an
arctic
, auroral, chill; the fourth contains six months of night.
What is gained by such a severe process of reduction? In these
condensed
transcriptions of experience, all ambiguities of twilight, poetry of misty horizons, flux and riddle of coast-lines, are suppressed in favour of
the immediacy of the great elements. One comes out of a cave, and faces the sky; one crosses the brow of a hill, and there is the Atlantic….
I sent a draft of this to Spencer-Brown, looking for permission to quote from his then unpublished book, and later phoned him. He sounded mildly interested in my poetic application of his words, and I arranged to call on him at his flat in Richmond. I found him to be a middle-aged man with a dark and intellectually hungry look, a shadow of D.H. Lawrence projected into abstract realms. He was very ready to expound his discoveries, though a little short with my mathematical ignorance; as a student, his IQ had been ‘off the clock’, he told me. He scribbled in the flyleaf of my proof copy of
Laws
of
Form
a little diagram of how
i
is
re-entered
into its defining equation, as mentioned above. He
identified
his ‘marked and unmarked states’ with the Yang and Yin of Taoism – concepts I had thought long worn away to nothing by mindless overapplication. But his counting device, a stack of
circuits
like the one described above that counts to two, each
feeding
its output into the next, and so registering a number in the binary system, was a very concrete application of his theories; it was patented, he told me, and used in the real world by British Rail for keeping track of the number of railway wagons entering and leaving tunnels. Spencer-Brown had developed this device in collaboration with his brother, whom he mentioned also as the discoverer of some abstruse equations for which he ‘had to go very far’. The impression I came away with of this brother was slightly mysterious; he seemed to combine an uncanny degree of intelligence with a certain mythical remoteness from the actual, like Holmes’s Mycroft.
Mathematics cohabited with mysticism in Spencer-Brown’s
bookshelves. I noticed J.W. Dunne’s
An
Experiment
With
Time,
which had caused a commotion in the 1920s by purporting to make precognitive dreams scientifically respectable. Dunne argues that since time passes, there must be another time with which to measure how fast it passes, and yet another to measure the passing of that, and so on; also, we have a consciousness, a consciousness of that consciousness, etc., corresponding to this infinite number of time-dimensions, and that these higher-dimensional
consciousnesses
are (naturally!) able to see at least some way into the future of ordinary everyday time. H.G. Wells had been impressed by Dunne at first but later said his thesis was ‘an entertaining paradox expanded into a humourless obsession’. I had early learned to sneer at it, but now Spencer-Brown put me right; Dunne had grasped the importance of ‘recursion’ (the sort of snake-
swallowing
-its-own-tail process exemplified by Spencer-Brown’s
expressions
that re-enter themselves), and had merely lacked the mathematics to develop it.
Peter Joseph’s exhibition was due to open at the Lisson Gallery soon thereafter, and I invited Spencer-Brown to the opening. M and I arrived a little late, and found him looking rather adrift among the gallery-going crowd. We stayed him with
conversation
. I asked – it was out of order as party chitchat, but I did want to know, having been fiddling with the question inconclusively – if his arithmetic of indications was isomorphic with the arithmetic of the null set and the universal set. (‘Isomorphic’ is jargon for ‘structurally identical’.) He concentrated inwardly for a few
seconds
before answering, ‘Yes.’ He seemed a little put out, so I
hastened
to add, ‘I suppose no one ever thought to write down the arithmetic of the null set and the universal set.’ ‘Quite!’ he replied. Later an exotic girl, prime ornament of the art-gallery set of that
season, black with a bloom of gold-dust, came in, and we all turned to admire her. M said she could see purple smoke rising from her, and Spencer-Brown explained that that was because she was seeing her directly; if the light-level had been lower the girl’s ‘essential body’ would have been visible hovering above her head.