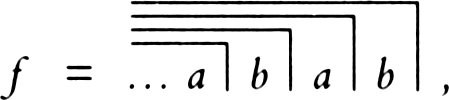
My Time in Space (17 page)

What shape is space? And, as it is known to be expanding, will it continue to do so, or will it someday begin to contract again, perhaps into the state it started from, something hardly more than a point? These are the most enormous, if least pressing, of empirical questions, and I am exhilarated by the fact that our age is the first with the technical wit to answer them. In 1999 astronomers analyzing the motions of distant galaxies and the brightness of supernovas announced (with due tentativeness) their long-awaited findings: spacetime is either flat or very nearly so, and will expand at an accelerating rate for ever. Consider what this means: since the universe came into existence a finite length of time ago, its past is as nothing, quite literally, in mathematical terms, in comparison with what is to come. More marvellous yet, this will always be the case. Even if we ourselves perish in its cold, and Pascal’s lamplight fades, the world is eternal dawn.

But, should the universe prove the astronomers wrong by
bringing
itself to a full stop and disappearing, and even had it never existed at all, Pascal’s theorem would still be true. Had no mind ever conceived a conic and no hand ever drawn a hexagon, it would still be the case that, ‘If a hexagon is inscribed in a conic, the points of intersection of opposite sides will lie on a line.’ The truths of mathematics transcend the existent, and by their own account of it mathematicians have to make strange journeys to bring those truths home to us; they talk of dream, revelation, intuition, and they claim to waste little time trying to prove results that later turn out to be false; they have a nose for the genuine article of faith. The logical processes of proof may have little to do with this primary capture of truth; after the event, it may be the labour of years to construct a proof others can follow.

My own capabilities in this regard are modest; Cambridge judged correctly in awarding me a second-class degree, and since I left the field I have forgotten most of the standard results and ready-to-hand techniques that are second nature to the
professional
. But I have had glimmers of illumination; in the days when I was a visual artist now and again an odd little theorem would turn up in my preliminary workings for an abstract painting, like a freebie toy in a cornflakes packet. And though my head is bloodied against the bars of my limitations I delight in following the creative mathematician so far as I can into that glorious unknown, which I picture not as a chill Platonic heaven but an Aladdin’s cave, a darkness full of dazzlement. But are there cracked bowls and counterfeit jewels among its treasures? Are the mathematicians right in supposing that the goods to which they
have their mysterious access are all sound? Sometimes it takes
generations
to come to a judgement on particular cases.

During my London years, since no one bought my artworks, I had to help support myself and my painting habit by drawing diagrams for technical books. One day in 1968 a typescript by a G. Spencer Brown
*
arrived from the publishers Messrs George Allen & Unwin, with the author’s rough sketches to guide me in illustrating it.
Laws
of
Form
was the take-it-or-leave-it title. The meat of the text began with:

and it culminated with what appeared to be a derivation of the basic rules of logic from two drastically simple formulae. The steps in between looked like no mathematics I had ever come across; for instance:

according to which something rather complicated equals a blank. I was intrigued, and read it closely, following through the
argument
line by line, and came to believe that despite the Age-
of-Aquarius
tone of some of its pronouncements (‘A recognisable aspect of the advancement of mathematics consists in the
advancement
of the consciousness of what we are doing, whereby the covert becomes the overt. Mathematics is in this respect
psychedelic.’)
this was hard-hat mathematics, with genuine applications to electrical engineering, and that it did actually found logic on the formal properties of the elementary act of drawing a distinction.

Laws
of
Form
uses the symbol
to mark a distinction; one could use a closed box just as well since it makes a distinction between its inside and its outside, but Spencer-Brown’s mark is typographically handier. An innovative if unnerving move is to use a blank to represent the state of affairs before a distinction is drawn. A distinction allows us to name the states or values
distinguished
. Drawing the same distinction twice is no more
informative
than drawing it once; if a name is called and then called again, it still indicates the same state; so:

The mark can be understood as an instruction to cross the
boundary
, say from inside to outside. Crossing the boundary again takes you back to your first state, or, ‘to recross is not to cross’;
Spencer-Brown
writes this as:

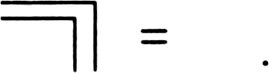
(The two marks are drawn slightly separated for clarity, but should be thought of as occupying exactly the same position.) These two equations are the ‘primitive equations’ of a very simple arithmetic, in which there are only two elements, a mark and the absence of a mark. By applying these equations repeatedly it is possible to work out whether more complicated arrangements of marks within marks, such as that on the previous page, are equivalent to a single mark or to the absence of a mark.

So a calculus – that is, a symbolic system within which
calculations
can be made – is born. Within a few pages it flowers into theorems of some complexity. Very soon one can draw
conclusions
about unspecified arrangements of marks; if the letter
p
stands for such an arrangement, it is easily proved that

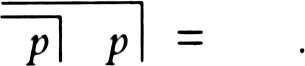
(This follows from the fact that any arrangement is equivalent to
or to.) Not quite so simple, but provable in the same way, is the equation:

Already the arithmetic has developed into an algebra, with these two equations as its primitive propositions. Now we jump to another level of considerations with endless arrangements such as