The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (36 page)

Finally, we can imagine creating dark matter right here at home, at the LHC. If the Higgs couples to dark matter, and the dark matter isn’t too heavy, one of the ways the Higgs can decay is directly into WIMPs. We can’t detect the WIMPs, of course, since they interact so weakly; any that are produced will fly right out of the detector, just as neutrinos do. But we can add up the total number of observed Higgs decays and compare it with the number we expect. If we’re getting fewer than anticipated, that might mean that some of the time the Higgs is decaying into invisible particles. Figuring out what such particles are, of course, might take some time.

An unnatural universe

Dark matter is solid evidence that we need physics beyond the Standard Model. It’s a straightforward disagreement between theory and experiment, the kind physicists are used to dealing with. There’s also a different kind of evidence that new physics is needed: fine-tuning within the Standard Model itself.

To specify a theory like the Standard Model, you have to give a list of the fields involved (quarks, leptons, gauge bosons, Higgs), but also the values of the various numbers that serve as parameters of the theory. These include the masses of the particles as well as the strength of each interaction. The strength of the electromagnetic interaction, for example, is fixed by a number called the “fine-structure constant,” a famous quantity in physics that is numerically close to 1/137. In the early days of the twentieth century, some physicists tried to come up with clever numerological formulas to explain the value of the fine-structure constant. These days, we accept that it is simply part of the input of the Standard Model, although there is still hope that a more unified theory of the fundamental interactions would allow us to calculate it from first principles.

Although all of these numbers are quantities we have to go out and measure, physicists still believe that there are “natural” values for them to take on. That’s because, as a consequence of quantum field theory, the numbers we measure represent complicated combinations of many different processes. Essentially, we need to add up different contributions from various kinds of virtual particles to get the final answer. When we measure the charge of the electron by bouncing a photon off it, it’s not just the electron that is involved; that electron is a vibration in a field, which is surrounded by quantum fluctuations in all sorts of other fields, all of which add up to give us what we perceive as the “physical electron.” Each arrangement of virtual particles contributes a specific amount to the final answer, and sometimes the amount can be quite large.

It would be a big surprise, therefore, if the observed value of some quantity was very much smaller than the individual contributions that went into creating it; that would mean that large positive contributions had added to large negative contributions to create a tiny final result. It’s possible, certainly; but it’s not what we would anticipate. If we measure a parameter to be much smaller than we expect, we declare there is a fine-tuning problem, and we say that the theory is “unnatural.” Ultimately, of course, nature decides what’s natural, not us. But if our theory seems unnatural, it’s a sign that we might need a better theory.

For the most part, the parameters of the Standard Model are pretty natural. There are two glaring exceptions: the value of the Higgs field in empty space, and the energy density of empty space, also known as the “vacuum energy.” Both are much smaller than they have any right to be. Notice that they both have to do with the properties of empty space, or the “vacuum.” That’s an interesting fact, but not one that anyone has been able to take advantage of to solve the problems.

The two problems are very similar. For both the value of the Higgs field and the vacuum energy, you can start by specifying any value you like, and then on top of that you imagine calculating extra contributions from the effects of virtual particles. In both cases, the result is to make the final result bigger and bigger. In the case of the Higgs field value, a rough estimate reveals that it should be about 10
¹⁶
—ten quadrillion—times larger than it actually is. To be honest, we can’t be too precise about what it “should be,” since we don’t have a unified theory of all interactions. Our estimate comes from the fact that virtual particles want to keep making the Higgs field value larger, and there’s a limit to how high it can reasonably go, called the “Planck scale.” That’s the energy, about 10
¹⁸
GeV, where quantum gravity becomes important and spacetime itself ceases to have any definite meaning.

This giant difference between the expected value of the Higgs field in empty space and its observed value is known as the
“
hierarchy problem.” The energy scale that characterizes the weak interactions (the Higgs field value, 246 GeV) and the one that characterizes gravity (the Planck scale, 10
¹⁸
GeV) are extremely different numbers; that’s the hierarchy we’re referring to. This would be weird enough on its own, but we need to remember that quantum-mechanical effects of virtual particles want to drive the weak scale up to the Planck scale. Why are they so different?

Vacuum energy

As if the hierarchy problem weren’t bad enough, the vacuum energy problem is much worse. In 1998, astronomers studying the velocities of distant galaxies made an astonishing discovery: The universe is not just expanding, it’s accelerating. Galaxies aren’t just moving away from us, they’re moving away faster and faster. There are different possible explanations for this phenomenon, but there is a simple one that is currently an excellent fit to the data: vacuum energy, introduced in 1917 by Einstein as the “cosmological constant.”

The idea of vacuum energy is that there is a constant of nature that tells us how much energy a fixed volume of completely empty space will contain. If the answer is not zero—and there’s no reason it should be—that energy acts to push the universe apart, leading to cosmic acceleration. The discovery that this was happening resulted in a Nobel Prize in 2011 for Saul Perlmutter, Adam Riess, and Brian Schmidt.

Brian was my office mate in graduate school. In my last book,
From Eternity to Here
, I told the story of a bet he and I had made back in those good old days; he guessed that we would not know the total density of stuff in the universe within twenty years, while I was sure that we would. In part due to his own efforts, we are now convinced that we do know the density of the universe, and I collected my winnings—a small bottle of vintage port—in a touching ceremony on the roof of Quincy House at Harvard in 2005. Subsequently, Brian, who is a world-class astronomer but a relentlessly pessimistic prognosticator, bet me that we would fail to discover the Higgs boson at the LHC. He recently conceded that bet as well. Both of us having grown, the stakes have risen accordingly; the price of Brian’s defeat is that he is using his frequent-flyer miles to fly me and my wife, Jennifer, to visit him in Australia. At least Brian is in good company; Stephen Hawking had a $100 bet with Gordon Kane that the Higgs wouldn’t be found, and he’s also agreed to pay up.

To explain the astronomers’ observations, we don’t need very much vacuum energy; only about one ten-thousandth of an electron volt per cubic centimeter. Just as we did for the Higgs field value, we can also perform a back-of-the-envelope estimate of how big the vacuum energy should be. The answer is about 10
¹¹⁶
electron volts per cubic centimeter. That’s larger than the observed value by a factor of 10
¹²⁰
, a number so big we haven’t even tried to invent a word for it. The hierarchy problem is bad, but the vacuum energy problem is numerically much worse.

Understanding the vacuum energy is one of the leading unsolved problems of contemporary physics. One of the many contributions that makes the estimated vacuum energy so large is that the Higgs field, sitting there with a nonzero value in empty space, should carry a lot of energy (positive or negative). This was one of the reasons Phil Anderson was wary of what we now call the Higgs mechanism; the large energy density of a field in empty space seems to be incompatible with the relatively small energy density that empty space actually has. Today we don’t think of this as a deal breaker for the Higgs mechanism, simply because there are also plenty of other contributions to the vacuum energy that are even larger, so the problem runs much deeper than the Higgs contribution.

It’s also possible that the vacuum energy is exactly zero, and that the universe is being pushed apart by a form of energy that is slowly decaying rather than strictly constant. That idea goes under the rubric of “dark energy,” and astronomers are doing everything they can to test whether it might be true. The most popular model for dark energy is to have some new form of scalar field, much like the Higgs, but with an incredibly smaller mass. That field would roll gradually to zero energy, but it might take billions of years to do it. In the meantime, its energy would behave like dark energy—smoothly distributed through space, and slowly varying with time.

The Higgs boson we’ve detected at the LHC isn’t related to vacuum energy in any direct way, but there are indirect connections. If we knew more about it, we might better understand why the vacuum energy is so small, or how there could be a slowly varying component of dark energy. It’s a long shot, but with a problem this stubborn we have to take long shots seriously.

Supersymmetry

A major lesson of the success of the electroweak theory is that symmetry is our friend. Physicists have become enamored with finding as much symmetry as they possibly can. Perhaps the most ambitious attempt along these lines comes with a name that is appropriate if not especially original: supersymmetry.

The symmetries underlying the forces of the Standard Model all relate very similar-looking particles to one another. The symmetry of the strong interactions relates quarks of different colors, while the symmetry of the weak interactions relates up quarks to down quarks, electrons to electron neutrinos, and likewise for the other pairs of fermions. Supersymmetry, by contrast, takes the ambitious step of relating fermions to bosons. If a symmetry between electrons and electron neutrinos is like comparing apples to oranges, trying to connect fermions with bosons is like comparing bananas to orangutans.

At first glance, such a scheme doesn’t seem very promising. To say that there is a symmetry is to say that a certain distinction doesn’t matter; we label quarks “red,” “green,” and “blue,” but it doesn’t matter which color is which. Electrons and electron neutrinos are certainly different, but that’s because the weak interaction symmetry is broken by the Higgs field lurking in empty space. If the Higgs weren’t there, the (left-handed parts of the) electron and electron neutrino would indeed be indistinguishable.

When we look at the fermions and bosons of the Standard Model, they look completely unrelated. The masses are different, the charges are different, the way certain particles feel the weak and strong forces and others don’t is different, even the total number of particles is completely different. There’s no obvious symmetry hiding in there.

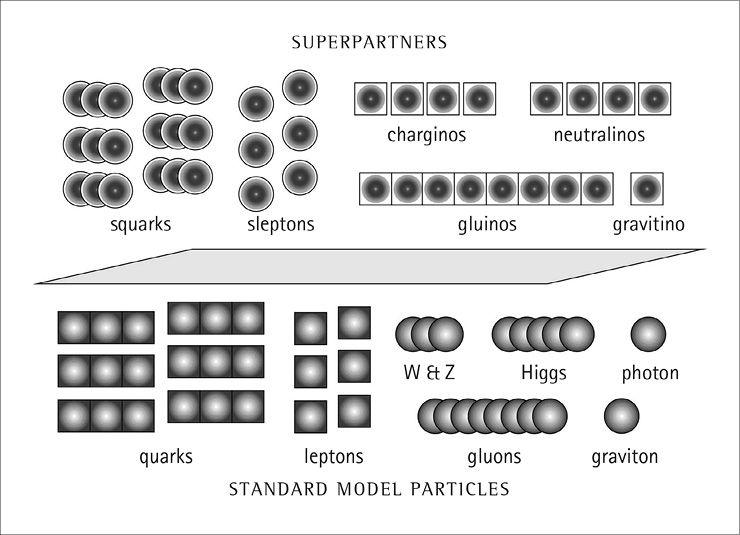
Physicists tend to persevere, however, and eventually they hit on the idea that all the particles of the Standard Model have completely new “superpartners,” to which they are related by supersymmetry. All of these superpartners are supposed to be very heavy, so we haven’t detected any of them yet. To celebrate this clever idea, physicists invented a cute naming convention. If you have a fermion, tag “s–” onto the beginning to label its boson superpartner; if you have a boson, tag “–ino” onto the end to label its fermion superpartner.

In supersymmetry, therefore, we have a new set of bosons called “selectrons” and “squarks” and so on, as well as a new set of fermions called “photinos” and “gluinos” and “higgsinos.” (As Dave Barry likes to say, I swear I am not making this up.) The superpartners have the same general features as the original particles, except the mass is much larger and bosons and fermions have been interchanged. Thus, a “stop” is the bosonic partner of the top quark; it feels both the strong and weak interactions, and has charge +2/3. Interestingly, in specific models of supersymmetry the stop is often the lightest bosonic superpartner, even though the top is the heaviest fermion. The fermionic superpartners tend to mix together, so the partners of the W bosons and the charged Higgs bosons mix together to make “charginos,” while the partners of the Z, the photon, and the neutral Higgs bosons mix together to make “neutralinos.”

Supersymmetry is currently an utterly speculative idea. It has very nice properties, but we don’t have any direct evidence in its favor. Nevertheless, the properties are sufficiently nice that it has become physicists’ most popular choice for particle physics beyond the Standard Model. Unfortunately, while the underlying idea is very simple and elegant, it is clear that supersymmetry must be broken in the real world; otherwise particles and superpartners would have equal masses. Once we break supersymmetry, it goes from being simple and elegant to being a god-awful mess.

There is something called the “Minimal Supersymmetric Standard Model,” which is arguably the least complicated way to add supersymmetry to the real world; it comes with 120 new parameters that must be specified by hand. That means that there is a huge amount of freedom in constructing specific supersymmetric models. Often, to make things tractable, people set many of the parameters to zero or at least set them to be equal. As a practical matter, all of this freedom means that it’s very hard to make specific statements about what supersymmetry predicts. For any given set of experimental constraints, it’s usually possible to find some set of parameters that isn’t yet ruled out.