Three Roads to Quantum Gravity (5 page)

However, classical logic demands that every statement be either true or false. Classical logic is therefore not a description of how we reason. Classical logic could be applied only by some being outside the universe, a being who could see the whole cosmos and count all its cats. But, if we insist on our principle that there is nothing outside the universe, there is no such being. To do cosmology, then, we need a different form of logic - one that does not assume that every statement can be judged true or false. In this kind of logic, the statements an observer can make about the universe are divided into at least three groups: those that we can judge to be true, those that we can judge to be false and those whose truth we cannot decide upon at the present time.

According to the classical view of logic, the question of whether a statement can be judged to be true or false is something absolute - it depends only on the statement and not on the observer doing the judging. But it is easy to see that this is not true in our universe, and the reason is closely related to what we have just said. Not only can an individual
observer only see light from one part of the universe; which part they can see depends on where they find themselves in the history of the universe. We can judge the truth or falseness of statements about the Spice Girls. But observers who live more than 14 billion years from us cannot because they will not have received any information that would even let them suspect the existence of such a phenomenon. So we must conclude that the ability to judge whether a statement is true or false depends to some extent on the relationship between the observer and the subject of the statement.

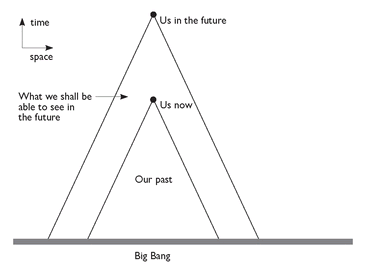
Observers in the future will be able to see more of the universe than we can see now. The diagonal lines represent the paths of light rays travelling from the past to us. Since nothing can travel faster than light, anything in our past that we can see or experience any effect of must lie within the triangle completed by the two diagonal lines. In the future we shall be able to receive light from farther away, and therefore see farther.

Furthermore, an observer who lives on Earth a billion years from now will be able to see much more of the universe, for they will be able to see 15 billion light years out into the universe rather than the 14 billion light years we can see. They will see everything we can see, but they will see much more because they will see farther (
Figure 5
). They may be
able to see many more cats. So, the list of statements they can judge to be true or false includes all that we can judge, but it is longer. Or consider an observer who lives 14 billion years after the big bang, as we do, but is 100 billion light years from us. Many cosmologists argue that the universe is at least 100 billion light years across; if they are right there is no reason for there not to be intelligent observers at that distance from us. But the part of the universe that they see has no overlap with the part of the universe that we see. The list of statements they can judge to be true or false is thus completely different from the list of statements that we here on Earth can judge to be true or false. If there is a logic that applies to cosmology, it must therefore be constructed so that which statements can be judged to be true or false depends on the observer. Unlike classical logic, which assumes that all observers can decide the truth or falsity of all statements, this logic must be observer-dependent.

In the history of physics it has often happened that by the time the physicists have been able to understand the need for a new mathematics, they found that the mathematicians had got there first and had already invented it. This is what happened with the mathematics needed for quantum theory and relativity and it has happened here as well. For reasons of their own, during the twentieth century mathematicians investigated a whole collection of alternatives to the standard logic we learned in school. Among them is a form of logic which we may call ‘logic for the working cosmologist’, for it incorporates all the features we have just described. It acknowledges the fact that reasoning about the world is done by observers inside the world, each of whom has limited and partial information about the world, gained from what they can observe by looking around them. The result is that statements can be not only true or false; they can also carry labels such as ‘we can’t tell now whether it’s true, but we might be able to in the future’. This cosmological logic is also intrinsically observer-dependent, for it acknowledges that each observer in the world sees a different part of it.

The mathematicians, it seems, were not aware that they were inventing the right form of logic for cosmology, so they
called it other names. In its first forms it was called ‘intuitionistic logic’. More sophisticated versions which have been studied more recently are known collectively as ‘topos theory’. As a mathematical formalism, topos theory is not easy. It is perhaps the hardest mathematical subject I’ve yet encountered. All of what I know of it comes from Fotini Markopoulou-Kalamara, who discovered that cosmology requires non-standard logic and found that topos theory was right for it. But the basic themes of it are obvious, for they describe our real situation in the world, and not only as cosmologists. Here in the real world, we almost always reason with incomplete information. Each day we encounter statements whose truth or falsity cannot be decided on the basis of what we know. And in the forms of our social and political life we recognize, often explicitly, that different observers have access to different information. We also deal every day with the fact that the truth or falsity of statements about the future may be affected by what we choose to do.

This has very profound implications for a whole host of issues. It means that to judge the rationality of our decisions, we do not have to pretend that there is some supernatural observer who knows everything: it is enough to demand that the different observers report what they see honestly. When this rule is followed we discover that when we and another person each have enough information to decide whether something is true or false, we always make the same decision.

Thus, the philosophers who attempted to ground ethics and science in the ultimate judgements of an all-knowing being were mistaken. We can live rationally without having to believe in a being who sees everything. We need only believe in the ethical principle that observers should communicate honestly what they see. If we stick to this, then the fact that there will always be questions that we cannot answer need not prevent us from coming to an agreement about how to understand those aspects of our world which we share in common.

So topos, or cosmological, logic is also the right logic for understanding the human world. It, and not Aristotle, must be the right basis for economics, sociology and political
science. I am not aware that anyone in these areas has taken up topos theory and tried to make it the foundation of their subject, although George Soros’s approach to economics, which he calls the theory of reflexivity, is certainly a start in the right direction. But we should not be surprised if both cosmology and social theory point us in the same direction. They are the two sciences that cannot be formulated sensibly unless we build into their foundations the simple fact that all possible observers are inside the systems they study.

S
o far I have said nothing at all about quantum theory. We have seen that even without it, doing cosmology requires a radical revision of our way of doing science - a revision that goes even to the foundations of logic. Any scientific form of cosmology requires a radical change in the logic we use, to take into account the fact that the observer is inside the universe. This requires us to build our theory so that from the beginning it takes into account a form of observer dependence. We must acknowledge that each observer can have only a limited amount of information about the world, and that different observers will have access to different information.

With this important principle in mind, we may turn to the problem of how to bring quantum theory into cosmology. ‘Hold it!’, I can hear the reader saying. ‘Quantum theory is confusing enough. Now I’m being asked to think about how to apply it to the universe as a whole! Where do I get off?’ That’s understandable, but, as I shall explain in this chapter, thinking about how to apply quantum theory to the universe as a whole may make quantum physics easier, not harder, to understand. The principles we have looked at in the first two chapters may very well be the key to making quantum theory comprehensible.

Quantum theory is puzzling because it challenges our standard ideas about the relationship between theory and observer. The theory is indeed so puzzling that there is no
universally accepted physical interpretation of it. There are many different points of view about what quantum theory really asserts about reality and its relationship to the observer. The founders of quantum theory, such as Einstein, Bohr, Heisenberg and Schrödinger, could not agree on these questions. Nor is the present-day situation any better, for now we have extra points of view that those guys, smart as they were, were not imaginative enough to foresee. There is now no more agreement about what quantum theory means than when Einstein and Bohr first debated the question in the 1920s.

It is true that there is only one mathematical formalism for the quantum theory. So physicists have no problem with going ahead and using the theory, even though they do not agree about what it means. This may seem strange, but it does happen. I have worked on projects in quantum gravity where everything went smoothly until the collaborators discovered one day over dinner that we had radically different understandings of the meaning of quantum theory. Everything went smoothly again after we had calmed down and realized that how we thought about the theory had no effect on the calculations we were doing.

But this is no consolation to the layperson, who does not have the mathematics to fall back on. With only the concepts and principles to go on, it must be very disconcerting to discover that different physicists, in their different books, offer very different versions of the basics of quantum theory.

Quantum cosmology helps rather than hinders because, as we are about to see, it limits the scope for possible interpretations of the quantum theory. If we stick to the principles introduced in the first two chapters, several of the approaches to the interpretation of quantum mechanics must be abandoned. Either that, or we must give up any idea that quantum theory can be applied to space and time. The principle that there is nothing outside the universe and the principle that in the future we shall know more do point to a new way of looking at quantum theory that is both simpler and more rational than many of the older ideas. As a result of applying quantum theory to cosmology, there has emerged over the last
few years a new approach to the problem of the meaning of quantum theory. This is what I want to communicate in this chapter.

Ordinary quantum theory is a theory of atoms and molecules. In the form developed originally by Bohr and Heisenberg, it required the world to be split into two parts. In one part was the system under study, which was described using the quantum theory, and in the other part lived the observer, together with whatever measuring instruments were needed to study the first system. This separation of the world into two parts is essential for the very structure of quantum mechanics. At the heart of this structure lies the superposition principle, which is one of the basic axioms of the quantum theory.

The superposition principle is not easy to understand, because it is formulated in seemingly abstract terms. If one is not careful it can lead to a kind of mysticism in which its meaning is over-interpreted far past what the evidence calls for. So we shall be careful, and spend some time looking at the statement of this important principle.

Let us first state it. The superposition principle says that if a quantum system can be found in one of two states, A and B, with different properties, it may also be found in a combination of them,
a
A +
b
B, where a and b are any numbers. Each such combination is called a superposition, and each is physically different.

But what does this actually mean? Let us break it down. The first thing to understand is what physicists mean when they talk about ‘states’. This one word contains almost the full mystery of the quantum theory. Roughly, we say that the state of a physical system is its configuration at a particular moment. For example, if the system is the air in the room, its state might consist of the positions of all the molecules together with their speeds and the directions of their motions. If the system is a stock market, the state is the list of the prices of all the stocks at a particular moment. One way to say this is that a state consists of all the information needed to completely describe a system at an instant of time.