Three Roads to Quantum Gravity (22 page)

Physics, like the other sciences, is the art of the possible. So I must add a rider here, which is that we do not really understand QED. We know the principles of the theory and we can deduce from them the basic equations that define the theory. But we cannot actually solve these equations, or even prove that they are mathematically consistent. Instead, to make sense of them we have to resort to a kind of subterfuge. We make some assumptions about the nature of the solutions - which, after more than fifty years, are still unproved - and these lead us to a procedure for calculating approximately what happens when photons and electrons interact. This procedure is called perturbation theory. It is very useful in that it does lead to answers that agree very precisely with experiment. But we do not actually know whether the procedure is consistent or not, or whether it accurately reflects what a real solution to the theory would predict. String theory is presently understood mainly in the language of this approximation procedure. It was invented by modifying the approximation procedure, rather than the theory. This is how people were able to invent a theory which is understood only as a list of solutions.

Perturbation theory is actually quite easy to describe. Thanks to Feynman, there is a simple diagrammatic means for understanding it. Picture a world of processes in which three things can happen. An electron may move from point A at one time to point B at another. We can draw this as a line, as in
Figure 33
. A photon may also travel, which is indicated by a dotted line in the figure. The only other thing that may happen is that an electron and a photon interact, which is indicated by the point where a photon line meets an electron line. To compute what happens when two electrons meet, one simply draws all the things that can happen, beginning with two electrons entering the scene, and ending with two electrons leaving. There are an infinite number of such processes, and we see a few of them in
Figure 34
. Feynman taught us to associate with each diagram the probability (actually the quantum amplitude, whose square is the probability) of that process. One can then work out all the predictions of the theory.

The basic processes in the theory of electrons and photons (called quantum electrodynamics, or QED for short.) Electrons and photons can move freely in spacetime, or they can interact in events in which an electron absorbs or emits a photon.

In the language of these diagrams, now known appropriately as Feynman diagrams, it is very easy to explain what string theory is. The basic postulate of the theory is that there are no particles, only strings moving in space. A string is just a loop drawn in space. It is not made of anything, just as a particle is thought of as a point and nothing else. There is only one kind of string, and the different kinds of particle are postulated to be nothing but different modes of vibration of these loops. So, as shown in
Figure 35
, photons and electrons are to be thought of just as different ways in which a string can vibrate. When a string moves in time it makes a tube rather than a line (
Figure 35
). Two strings can also join and merge into one (
Figure 36
), or one string can split into two. All the interactions that occur in nature, including those of photons and electrons, can be interpreted in terms of these splittings and joinings. We can see from these pictures that string theory gives a very satisfactory unification and simplification of the physical processes represented in Feynman diagrams. Its main virtue is that it gives a simple way of finding theories that make consistent physical predictions.

The processes illustrated in
Figure 33
are put together to make Feynman diagrams, which are pictures of the possible ways a process can happen. Shown here are some of the ways in which two electrons can interact simply by absorbing and emitting photons. Each one is a story that is a possible piece of the history of a universe.

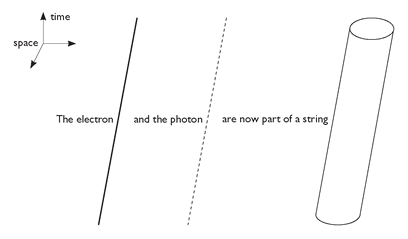
In string theory there is only one kind of thing that moves, and that is a string - a loop drawn in space. Different modes of vibration of the string behave like the different kinds of elementary particle.

All the different kinds of interaction between particles are interpreted in string theory in terms of the splitting and joining of strings.

The trouble with Feynman’s method is that it always leads to infinite expressions. This is because there are loops in the diagrams where particles are created, interact, and are then destroyed. These are called virtual particles because they exist only for a very short time. According to the uncertainty principle, because virtual particles live for a very short time
they can have any energy, as the conservation of energy is suspended during their brief lives. This creates big problems. One has to add up all the diagrams to get the overall probability for the process to occur, but if some particles can have any energy between zero and infinity, then the list of possible processes one has to add up will be infinite. This leads to mathematical expressions that are no more than complicated ways of writing the number infinity. As a result, Feynman’s method seems at first to give nonsensical answers to questions about the interactions of electrons and photons.

Quite ingeniously, Feynman and others discovered that the theory was giving silly answers to only a few questions, such as ‘What is the mass of the electron?’ and ‘What is its charge?’ The theory predicts that these are infinite! Feynman figured out that if one simply crosses out these infinite answers wherever they appear, and substitutes the right, finite answer, the answers to all other questions become sensible. All the infinite expressions can be removed if one forces the theory to give the right answer for the mass and the charge of the electron. This procedure is called renormalization. When it works for a theory, that theory is called renormalizable. The procedure works very well for quantum electrodynamics. It also works for quantum chromodynamics, and for the Weinberg-Salam theory, which is our theory of radioactive decay. When this procedure does not work, we say that a theory is not renormalizable - the method fails to give a sensible theory. This is actually the case for most theories; only certain special ones can be made sense of by these methods.

The most important theory that cannot be made sense of in this way is Einstein’s theory of gravity. The reason has to do with the fact that arbitrarily large energies can appear in the particles moving inside the diagrams. But the strength of the gravitational force is proportional to the energy, because energy is mass, from Einstein, and gravity pulls on mass, from Newton. So the diagrams with larger energies give correspondingly larger effects. But according to the theory, the energies inside the diagrams can be arbitrarily large. The result is a kind of runaway feedback process in which we lose all control over what is happening inside the diagrams. No
one has ever found a way to describe a gravitational theory in the language of particles moving around Feynman diagrams. But in string theory one can make sense of the effects of gravity. This is one of its great achievements. As with the older theories, there are many string theory variants that lead to infinite expressions for every physical process, and these must be discarded. What is left is a set of theories that have no infinities at all. One does not have to play any games to isolate infinite expressions for masses and throw them out. There are just two possible kinds of string theory: inconsistent and consistent. And all the consistent ones appear to give finite and sensible expressions for all physical quantities.

The list of consistent string theories is very long. There are consistent string theories in all dimensions from one to nine. In nine dimensions there are five different kinds of consistent string theory. When we get down to the three-dimensional world we seem to live in, there are at least hundreds of thousands of different consistent string theories. Most of these theories come with free parameters, so they do not make unique predictions for things like the masses of the elementary particles. Each consistent string theory is very tightly structured. Because all the different kinds of particle arise from vibrations of the same fundamental objects, one is not generally free to choose which particles are described by the theory. There are an infinite number of possible vibrations and hence of possible particles, although most of them will have energies which are too large to observe. Only the lowest modes of vibration correspond to particles with masses we could observe. A remarkable fact is that the particles that correspond to the lowest modes of vibration of a string always include the broad categories of particles and forces we do observe. The other modes of vibration correspond to particles with masses of around 10
¹⁹
times the mass of the proton. This is the Planck mass, which is the mass of a black hole the size of a Planck length.

However, there still are issues which must be addressed if string theory is to describe our universe. Many string theories predict the existence of particles which have so far not been seen. Many have problems keeping the strength of the
gravitational force from varying in space and time. And almost all consistent string theories predict symmetries among their particles beyond those that are seen. The most important of these are
supersymmetries
.

Supersymmetry is an important idea, so it is worth while making a detour here to discuss it. To understand supersymmetry one must know that elementary particles come into two general types: bosons and fermions. Bosons, which include photons and gravitons, are particles whose angular momentum, when measured in units of Planck’s constant, are simple integers. Fermions, which include electrons, quarks and neutrinos, have angular momenta that come in units of one-half. Fermions also satisfy the Pauli exclusion principle, which states that no two of them can be put in the same state. Supersymmetry requires fermions and bosons to come in pairs consisting of one of each, with the same mass. This is definitely not observed in nature. If there were such things as bosonic electrons and quarks, the world would be a very different place, for the Pauli exclusion principle would have no force, and no form of matter would be stable. If supersymmetry is true of our world, then it has been
spontaneously broken
, which is to say that the background fields must confer a large mass on one member of each pair and not on the other. The only reason to entertain the idea of such a strange symmetry is that it seems to be required for most, if not all, versions of string theory to give consistent answers.