X and the City: Modeling Aspects of Urban Life (47 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

It is possible to classify these urban density profiles in terms of the magnitude and sign of the parameter combination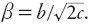 Specifically, the sequence “youth, early maturity, late maturity, old age” is characterized by Newling (1969) as corresponding to the
Specifically, the sequence “youth, early maturity, late maturity, old age” is characterized by Newling (1969) as corresponding to the
β
-intervals
*
(−∞, −1), (−1, 0), (0,1), and (1, ∞). This can be seen in a qualitative manner from
Figure 16.1
by mentally imagining these four stages of development to be, successively, the curve to the right of the ordinates
r
= 2, 1, 0.3, and 0. But from where do these intervals for
β
come? It’s all to do with points of inflection. Simply put, points of inflection in the graph of
ρ
(
r
) occur when there is a change of concavity (if those points are in the domain of the profile). From equation (16.4) such points occur at

It can be seen that if
b
< −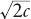 , i.e.,
, i.e.,
β
< −1, then there are no points of inflection and
ρ
(
r
) decreases monotonically from the central business district outward (youthful city). If −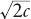 <
<
b
< 0, (−1 < β < 0) or 0 <
b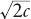 (0 <
(0 <
β
< 1) there is a single point of inflection (in early and late maturity, respectively). Finally, if
b
>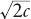 (
(
β
> 1) there are two such points and the full density crater profile is evident (aging city).
There can be variations on this theme using the concept of a “traveling wave of metropolitan expansion.” We can illustrate the stages of city development by positing a traveling pulse of “shape”
ρ
(
r
) moving outward with speed
v
, that is,

This can be interpreted as a point of constant density moving out radially with speed
v
. In principle
v
may itself be a function of time; in any case, as the city develops in time, the shape of the density profile may change in accordance with the above equation.
Returning to the basic form (16.4), we now examine the density profile when some or all of the parameters
A
(=
ρ
0
),
b
, and
c
may be functions of time. In view of the
spatial
behavior exhibited by
ρ
(
r
) from (16.4), that is, initially increasing to a maximum, then decreasing monotonically, Newling (1969) chose the same
temporal
form for
ρ
0
(
t
):

ρ
0
now being a constant. Furthermore, he chose
b
to be a linear function,
b
(
t
) =
b
0
+
gt
, where
g
and
c
are constants. From equation (16.4) (noting again the change in sign for
b
from equation (16.1)) it can be seen that
b
=
ρ
′(0)/
ρ
(0), the prime referring to a spatial derivative. Thus

Proceeding as with the derivation of equation (16.6) gives the corresponding result for the radius of the urbanized area (now at time
t
) as
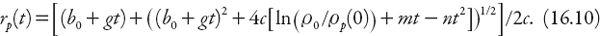
The “speed” of urban expansion can be then defined as
r
p
(
t
)/
t
for
t
> 0. This type of model has also been used in ecological contexts, studying the spread of animal and insect populations (as well as diseases) in so called reaction-diffusion models.
Now let’s use the density profile (16.4) to compute some overall population levels. As in equation (16.2), we may compute the total metropolitan population in a disk of radius
R
0
. It is given by the integral