X and the City: Modeling Aspects of Urban Life (46 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

(This is called the “civic mass” in
Chapter 17
.) An estimate of the total population in a spatially infinite city(!) can be found from the limiting case
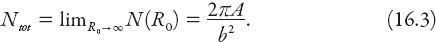
This is not such an unreasonable result as might be first thought, because the population density (16.1) is decreasing exponentially fast. Obviously the result
is formally unchanged if
A
and
b
are time-dependent; for example, if the data justified it we could choose both parameters to be linearly decreasing functions of time. This will no doubt vary from city to city and we do not pursue it here.
In
Tables 16.1
–
16.4
,
A
is expressed per square mile in thousands, and
b
in (miles)
−1
. Cities have two fundamental modes of growth: up and out! Of course, in practical terms growth is usually a combination: there are ultimate limits on both of them. The parameter
A
is a measure of “up” in the sense of central density;
b
is a measure of how far “out” growth occurs—the smaller
b
is, the more decentralized the city becomes—this is often referred to as “urban sprawl.” Notice that the total population is proportional to
A
but inversely proportional to the square of the parameter
b
. The expression for
N
tot
based on equation (16.3) is generally of the right order of magnitude, particularly for London, but it does overestimate populations in later years, particularly for Chicago and New York. This partly because of the uncertainty of densities at small values of
R
, and also because cities are decidedly not circularly symmetric (as the first paragraph in this section implies)! Political and not just natural boundaries also play a role in urban development.
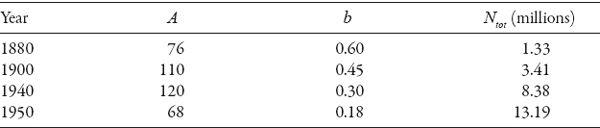
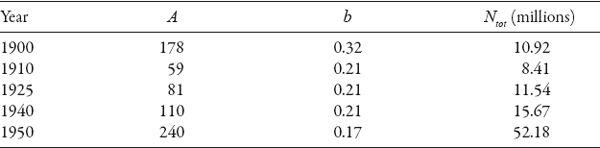
Generally, the value of the central density
ρ
(0) =
A
decreased, and so did
b
, meaning that the population of London became more decentralized. This trend is not always realized (at least, according to the limited data listed in Montroll and Badger (1974)). The corresponding data for Chicago, Paris, and New York, are shown in
Tables 16.2
–
16.4
.
Notice the precipitous drop in both parameters for London and Rome following the end of World War II.
T
ABLE
16.1.
Estimated population of London in the period 1801–1951 (based on equation (16.3))

T
ABLE
16.2.
Estimated population of Chicago in the period 1880–1950 (based on equation (16.3)
T
ABLE
16.3.
Estimated population of Paris in the period 1817–1946 (based on equation (16.3))

T
ABLE
16.4.
Estimated population of New York in the period 1900–1950 (based on equation (16.3))
According to Montroll and Badger (1974), the British archaeologist Sir Leonard Woolley estimated that the ancient city of Ur had an average density of 125,000 people per square mile at the height of its mature phase, around 2000 B.C. The density per square mile for parts of fourteenth-century Paris was 140,000, as was true for parts of London in 1700. By 1900, parts of New York’s Lower East Side had reached densities of 350,000 per square mile, but even this is small compared with many non-Western cites. If
A
increases while
b
remains constant, this can be accomplished quite easily over time. Thus parts of Hong Kong reached densities of about 800,000 per square mile; such high densities correspond to about one person for every four square yards!
Exercise:
Verify this last statement.
One problem with the density profile (16.1) is that it cannot reproduce the so-called “density crater” for the resident population in a large metropolitan area. This phenomenon means that the maximum population density occurs, not in the central region but in a ring surrounding the city center. This can be accomplished with the function
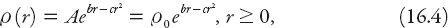
where
b
> 0,
c
>, and the maximum density occurs at radius
r
=
b
/2
c
. (Note that
b
is now of opposite sign to its counterpart in (16.1).) A graph of the normalized density function
ρ
n
(
r
) =
ρ
(
r
)/
ρ
0
is shown in
Figure 16.1
for the simple choice of
b
=
c
= 1.
Equation (16.4) could represent the density of a city with an extensive central business district. Let’s investigate the properties of this profile in some detail. The maximum density is


Figure 16.1. Form of the normalized population density function (16.4).
We suppose that there is a fairly well defined “perimeter” of the urban area at
r
=
r
p
, for which
ρ
(
r
p
) =
ρ
p
. Solving equation (16.4) for
r
p
yields the result (since
ρ
0
>
ρ
p
for all realistic models of cities):
