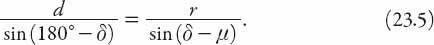X and the City: Modeling Aspects of Urban Life (71 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

Clearly,
D
> | cot
δ
| if is to be a real number. For
is to be a real number. For
δ
= 138° and
D
= 2 we find that sin ≈ ±0.557. Since
≈ ±0.557. Since
R
= 0 in the second quadrant, we obtain ≈ 2.55 radians, or approximately 146°. The limiting case of no loop occurs for
≈ 2.55 radians, or approximately 146°. The limiting case of no loop occurs for = 180°, and from equation (23.4) this corresponds to
= 180°, and from equation (23.4) this corresponds to
D
= | cot
δ
| ≈ 1.11. This limiting case is also shown in
Figure 23.5
.
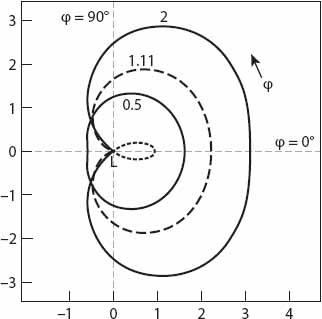
Figure 23.5. Polar diagram for the position of the bow as seen by the observer, based on equation (23.3). In decreasing order of size the graphs correspond respectively to
D
= 2, 1.11, and 0.5. In each case the “rainbow angle” is
δ
= 138°.
L
is at the center of any circle
R
= constant, and the observer is located on the horizontal axis at relative distance
D
from the base of the lighthouse.
Exercise:
Derive equation (23.4).
=
θ
: HALOS IN LIGHTHOUSE BEAMS
To see halos in such beams, there must be ice crystals present and we must turn around to face the lighthouse. Strictly speaking, as with the rainbows, these are
slices
of halos because of the narrowness of the beam. And as with solar and lunar halos, it may be necessary to block out the source of light in order to see a halo clearly. The 22° halo in particular appears to be darker inside the “rim’, so the beam is likely to appear darker nearer to the lighthouse, with a brighter spot corresponding to the halo slice. The larger halo will also be associated with a bright spot on the beam. As can be seen from
Figure 23.6
, the observer
O
should be at a distance of at least
h
cot
θ
from the base of the lighthouse for halos to be visible. The angles for the 22° and 46° halos are (not surprisingly)
θ
= 22° and 46°, so
d
> 2.48
h
and
d
> 0.97
h
, respectively (and approximately).
To compute the corresponding polar plots for the halos, we set
δ
= 22° and 46° respectively in equation (23.3). These are shown in
Figure 23.7
for
D
= 2. Note that, by contrast with the rainbow slices, the halos are visible for only a short period as the beam rotates over the observer.
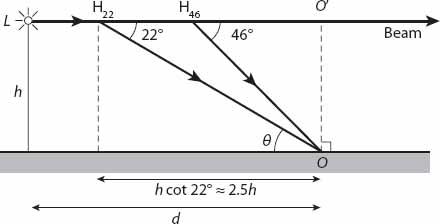
Figure 23.6. Geometry for halo formation in a stationary lighthouse beam.
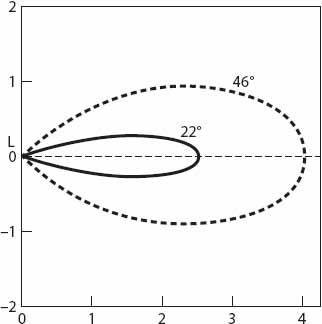
Figure 23.7. Polar diagram position of the halos as seen by the observer
O
at a distance of
D
= 5 units from the base of the lighthouse, using equation (23.3). In decreasing order of size the graphs correspond to
δ
= 46° and 22°.
=
θ
: RAINBOWS IN SEARCHLIGHT BEAMS
How do things change for the observer when looking at a searchlight beam? The situation is rather different because the searchlight will be close to the ground and pointing upward (unless we’re thinking about Alcatraz in its halcyon days), and therefore the beam will not be parallel to the ground. The notation in this case will differ a little from that in
Figure 23.3
; the angle
OSR
between the observer-searchlight line and the beam will be denoted by
μ
(see
Figure 23.8
). The distance from the searchlight to the rainbow slice is
r
. The angle between the beam and the vertical direction is
θ
, and the angles and
and
δ
are as defined in the previous section. It follows that the angle
SOR
=
δ
−
μ
. Applying the law of sines to the triangle
SOR
we have that
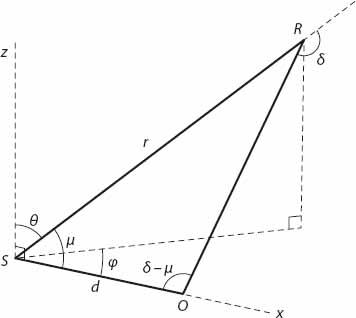
Figure 23.8. Geometry for rainbow “slice”
R
in a searchlight beam. The searchlight is at
S
and the observer is at
O
.