X and the City: Modeling Aspects of Urban Life (68 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

The quotient
q
(or “aspect ratio”) of the cigar’s short and long axes is

Let’s now find the equation of this cigar-shaped halo. The center of the circle,
O
′, in
Figure 22.8
is located at the point (0, −
R
cos
r
max
) or (0, −(cot
r
max
)/2). The equation of the circle is therefore

For the 22° halo, this angle is just
r
max
, so equation (22.4) can be rewritten as approximately
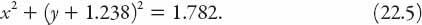

Figure 22.8. Relationship between the angular radius of a halo (
r
d
) with its center at a distance
d
from the light source. The length of the “cigar” is distance
BD
= 1,
ED
=
d
, angle
BCD
= 180° −
α
,
O′
is the center of the circle and
O
is the coordinate origin. Note from triangle
O′OD
that
α
=
r
max
.
This is the equation of the profile illustrated in
Figure 22.7
, noted earlier in “solid” form in
Figure 22.4
.
As noted above,
Figure 22.6
illustrates a cross section of the complementary cigar shape for other situations with much smaller “scattering angles” relative to the anti-source point (as opposed to the anti-solar point during the daytime). This includes both primary and secondary divergent-light rainbows. Each apple-shaped rainbow surface (c) and (d) can be regarded more accurately as a degenerate form of a torus, missing the central hole because the rotating circle intersects itself. This is well illustrated in the next chapter (
Figure 23.10
).
Complicated as these surfaces may seem, there is a very interesting two--dimensional subset of them that may be seen when the ground is covered with raindrops or dew (for “dewbows”) and frost or other ice crystals, such as diamond dust (ground-level cloud composed of tiny ice crystals; see
Appendix 11
).
Recall that a corresponding daytime phenomenon—“roadbows” (glass bead bows)—has been mentioned in
chapter 20
. As there, we consider first the simpler case of (nearly) parallel light from the sun (or occasionally the moon for “moonbows”). As noted above and in
Appendix 11
, sunlight scattered from raindrops can produce rainbows, and the scattered light appears to lie on the surface of a cone of semi-angle 42° with vertex at the observer’s eye. Now if the scattering droplets lie on the ground (as with dew), then that cone is effectively intercepted by a horizontal plane—the flat ground! If the solar altitude exceeds 42° the observer will see an elliptical “rainbow”; if it is exactly 42° the shape will be parabolic, but for an altitude less than 42° a hyperbolic rainbow or dewbow arc will be seen. This follows directly from the geometric definition of the conic sections. These same effects can be witnessed when flying above a cloud deck, by the way, for which the rainbow becomes a “cloudbow.”
= (
d
/2)csc
α
: DEWBOWS IN THE CITY
Now we will think about rainbows produced by sources of divergent light and scattered by droplets
on the ground
, that is, by dew. It is evident from
Figures 22.2
and
22.6
that the locus of scattering drops will be the major arc of a circle (such as
CFE
in
Figure 22.2
) in the plane containing the observer’s eye and the source of light. The chord
CE
will generally not be horizontal unless the lamp and eyes are at the same level. Therefore the intersection of this circular arc with the ground will be another circular arc of larger radius. If the distance
CE
between the light source and the observer’s eye is
d
, then the locus of all points subtending an angle
α
<
π
/2 is the major arc of a circle of radius
r
= (
d
/2)csc
α
. For generic primary and secondary rainbow angles of 42° and 51° these are approximately 0.75
d
and 0.64
d
respectively. Interestingly, therefore, in divergent light the radius of the secondary bow arc is
smaller
than that for the primary bow.
This is illustrated in
Figure 22.9
for an observer at
O
and a light source at
L
. When a nonvertical chord
LO
lies completely above the ground, and the circular arc is rotated around this chord, there is a point at which the arc is tangential to the ground, and thereafter the intersection with the ground splits into two points as illustrated in
Figure 22.9
. These two points of intersection move apart and then together, eventually tracing out the kidney-shaped curves illustrated in figures (a)–(d). The traces (e) and (f) correspond to the observer being directly below the light source, and above ground. In (e) the observer is low enough that the Minnaert “apple” surface traces out two concentric circular intersections; in (f) the surface is tangential to the ground because the observer is slightly higher above ground than in case (e). According to a report by Mattsson (1998), bows of the form (a)–(d) have been reported, but those like (e) and (f) have not. This is a challenge for the interested and observant reader!

Figure 22.9. Intersections of various “Minnaert cigar rainbow surfaces” with the ground for different configurations of observer (
O
) and light source (
L
). Redrawn from Mattsson (1998).
Regarding the corresponding “ground
halos
” produced by frost or diamond dust, I have been informed by Alexander Hauβmann that as young scientists, he and his friend Richard Löwenherz observed that in frost, only the 22° was frequently seen, whereas in diamond dust both the 22° and 46° halos were often present. They concluded that frost crystal faces were generally not well enough developed to ensure the consistent presence of the larger halo.
LIGHTHOUSES IN THE CITY?

Lighthouses in a town or city, you ask? Certainly; there are over a thousand in the United States (though many of them are no longer in use), and Michigan has the most lights of any state, with more than 150 past and present lights. A state-by-state listing of all U.S. lighthouses may readily be found online, as well as listings for lighthouses in Europe and elsewhere. Many of these are close to or within city boundaries. London’s only lighthouse (no longer functioning as such) is located at Trinity Quay Wharf in London’s docklands. By contrast, New York City has several. According to one online account [
40
]
When we think of lighthouses, we often conjure up images of majestic white towers perched on rocky outcroppings dotting the New
England coastline, or a stolid monolith announcing your arrival to the Outer Banks. But lighthouses in New York City? A city of soaring skyscrapers and hard concrete? What business do these anachronistic buildings of olden days have in New York, a city forever living on the cutting edge? Well, the truth is lighthouses do exist in New York City, and they have rightfully earned their place here, having helped build up this great city into what it has become.
Oh, by the way. If you still find the idea of lighthouses in a city too much of a stretch, consider
searchlights
instead. Once used primarily for military purposes, they now are widely used for advertising, fairs, festivals, and many other public events. Most of the features discussed below also apply to searchlight beams.
=
θ
: RAINBOWS IN LIGHTHOUSE BEAMS