X and the City: Modeling Aspects of Urban Life (69 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

Again, we can have some fun examining the “geometry of light” in this rather unusual context, and as in previous sections, we find some quite surprising results (see
Figure 23.1
). As a lighthouse (or searchlight) beam sweeps a rain-filled sky, a primary and often a secondary rainbow slice may often be noticed. As with a rainbow during the day, they are separated by a dark band (see
Figure 23.2
). Naturally, only those drops in the beam will scatter light into the observer’s eye. Subtle differences occur between the two types of beam, however, because a searchlight is close to the ground with a beam at an angle to the vertical direction, whereas the lighthouse is elevated relative to the observer, and has a horizontal beam. In each case, as the beam rotates about a vertical axis, the bows appear to slide up and down the beam.

Figure 23.1. Primary (and faint secondary) bow in the beam of the Westerhever Lighthouse in Nordfriesland (Germany). Photo by Achim Christopher.
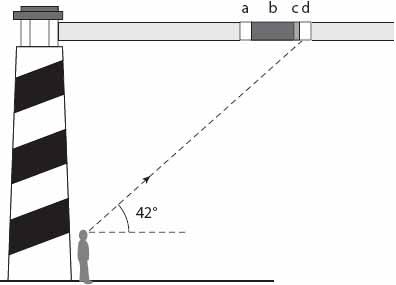
Figure 23.2. Rainbow “slices” seen in a lighthouse beam. The primary bow (or bright section) is at
d
, and if color is seen at all, the point
c
will be tinged with red. Alexander”s dark band is the segment at
b
, and the fainter secondary bow, if visible, will be at point
a.
(Redrawn from Floor (1982).
We will use
Figure 23.3
to explain this phenomenon for a lighthouse. Its beam, parallel to the ground, comes from a lamp
L
at height
h
above the ground. The observer at
O
is a distance
d
from the base of the lighthouse, standing directly under the beam at a particular instant of time. It is raining! The point
O
′ is a distance
h
vertically above
O
. From what we already know about rainbow formation, we know that if the angle
θ
≈ 42°, a primary bow (a better word might be slice) will be seen at
B
P
on the beam; similarly, if
θ
≈ 51°, a secondary bow will be located at
B
S
, though it will be fainter (and may not be visible at all). Certainly the beam will by contrast be brighter there than for the angular range 42° <
θ
< 51°, corresponding to the dark region between bows (Alexander’s dark band). This may be more readily seen in a lighthouse beam than in sunlight. The reddish edges of the bow define the ends of the dark band, though the colors may well be less evident because the eye is less sensitive to color at the (relatively) low light intensities present in a lighthouse beam.
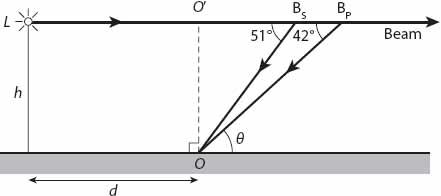
Figure 23.3. Geometry for rainbow formation in a stationary lighthouse beam.
When rainbows are produced by sunlight (or moonlight) the secondary bow appears higher in the sky than the primary. As such, it is often perceived to be farther away than the primary bow, but this is erroneous. While raindrops contributing to the secondary bow may or may not be farther away than those for the primary, the case for the lighthouse bows is definite and clear-cut: while the secondary bow appears higher in the sky, the drops giving rise to it
are
nearer the observer. This can be seen from
Figure 23.3
. The drops at
B
P
are a distance
OB
P
=
h
csc 42° ≈ 1.5
h
from the observer; those at
B
S
are at a distance
OB
S
=
h
csc 51° ≈ 1.3
h
. But this is for the case of a beam that is stationary with respect to the observer, so unless he or she runs in circles to stay directly under the beam, we need to consider a more general case!
=
R
(
 ): THE THREE-DIMENSIONAL CASE
): THE THREE-DIMENSIONAL CASEAs the beam rotates, the bows will appear to slide back and forth along the beam to maintain the rainbow angles of 42° and 51°, respectively. Let’s examine the geometry for an observer at
O
positioned outside the plane containing the lighthouse and its beam, as shown in
Figure 23.4
. For simplicity we consider that the beam in direction
LR
does not diverge significantly, and thus retains its intensity over its visible length.
R
is the location of a patch of rain scattering the light back toward the eye of the observer.
O
′ is a point directly
above the observer at the same height as the light source. The beam is at an angle from the line joining
from the line joining
O
to the base of the lighthouse.
δ
is the angle through which the light is deviated at
R
to be seen as a rainbow “slice” at
O
. For a primary bow,
δ
≈ 138°. Finally, angle
O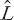 R
R
=
α
.

Figure 23.4. Geometry for “sliding rainbow” slices.
From
Figure 23.4
, applying the law of sines to triangle
LOR
, we find that
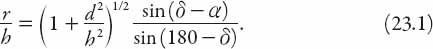
Application of the rule of cosines to triangles
LOR
and
LO’R
respectively yield
