125 Physics Projects for the Evil Genius (13 page)

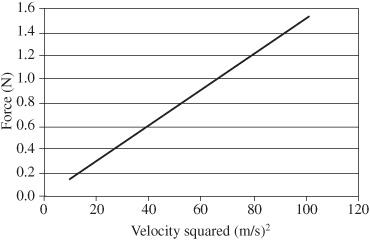
Figure 13-5
Centripetal force versus velocity squared
.

2. Either using Excel or plotting by hand makes a graph of
force
versus
velocity squared
. If the relationship is of the form expected, that graph should be a straight line. This is shown in
Figure 13-5
.

Given the data previously shown in
Figure 13-4
, we can determine that force varies inversely with the radius (string length) using the same techniques.

1. Have Excel determine the trendline for the expected data, as shown on the graph for the previous
Figure 13-4
.

2. Plotting force versus the reciprocal of radius (1/r) results in a straight line, as shown in
Figure 13-6
.

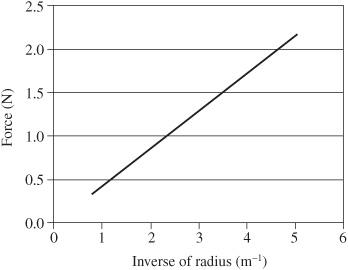
Figure 13-6
Centripetal force versus reciprocal of radius
.

This project works reasonably well and enables you to find the model for centripetal force using very simple equipment. The following are potential sources of errors that may impact your results:

1. Friction between the sting and the tube overstates the required force.
   
2. Air resistance results in a slightly slower value of velocity.
   
3. At slower speeds, the circle may not be perfectly horizontal and may have a complicating effect from gravity.
   

For any of the points you measured, compare the force you measured (by either the spring scale or the hanging mass) with the expected value for the centripetal force given by:

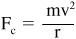
Centripetal force
keeps an object rotating in a circle. The centripetal force equals the mass of the object times the velocity squared divided by the radius.

In this project, you build a simple model of a planet going around the sun. This model exhibits many of the physical properties found throughout the solar system. You can discover for yourself the basic principles of planetary motion as did Copernicus and Kepler, except you won’t have to spend years squinting through a telescope on cold winter nights in the middle of the night to do this. This model also provides an intuitive way to visualize Einstein’s theory that gravity is the result of a mass curving space.

• bucket or other circular frame
  
• sheet of Latex, large enough to cover the opening of the bucket
  
• mass (roughly 50 g)—a 1-inch diameter spherical steel ball would be ideal because it can position itself in the center of the sheet
  
• marbles, small steel balls
  

1. Stretch the Latex on the bucket. Remove the wrinkles.
   
2. Roll the marble across the sheet and observe the path it takes.
   
3. Now, place the mass in the center of the sheet. This should cause the sheet to become noticeably distorted. If this is not the case, it may be necessary to increase the mass, but avoid tearing the sheet. The central mass should maintain a fixed position, which can be facilitated, if necessary, by a little tape.
   
4. Roll a marble in a circular path around the central mass.
   
5. Observe the motion of the marble. See
   Figure 14-1
   .
   
6. Observe what happens if the marble is rolled faster or slower in a given path. What happens if the marble is closer or farther from the central mass?
   

The key observation is that the path followed by the marble is an ellipse. The path may appear circular, but elliptical paths are certainly possible. This is comparable to one of Kepler’s observations concerning planetary motion.

Kepler also observed that the closer a planet gets to the sun, the faster it goes. The marbles in this experiment exhibit the same property.

If the marble is given a velocity that is too high, it will not follow the type of elliptical orbit followed by the planets around the sun but, rather, the open hyperbolic orbit followed by meteors.

Figure 14-1

Kepler’s law can be derived by equating the centripetal force that keeps a planet in orbit to the gravitational attraction between the planet and the sun. The depression created by the central mass exerts a force on the circulating marble that varies with position. Although this force does not exactly decrease with the inverse square of the distance, as does the gravitational attraction between a planet and the sun, it does provide a good approximation.

This experiment also provides an analogy for understanding an aspect of Einstein’s theory of general relativity. The idea is that what we call gravity is really a distortion in space caused by the presence of a mass. The distortion of the sheet can be thought to represent the distortion in space, which guides the path of a planet going around the sun. As far-fetched as this may seem at first, light from stars emerging from behind the sun has been observed by astronomers to follow a bent path caused by the sun’s mass, confirming Einstein’s prediction.

Objects in motion around a central mass follow an elliptical path. The closer they get to the central mass, the faster they go.

Gravitational attraction can be thought of as a distortion of space caused by the presence of the mass.

What determines how fast a car can safely go around a curve and not skid on the road? This project explores turning and friction, and how the two are related.

• board (approximately) 36 inches by 4 inches by ¾ inch (Other shapes, including a circularly shaped board or a turntable, can also be used.)
  
• vertical pole, such as a ring stand, to serve as a pivot point
  
• a few closely matched toy cars, such as Matchbox cars
  

Figure 15-1
Position of cars before rotation
.

1. Drill a hole in the center of the board. The hole should be large enough to allow the board to freely rotate on the post.
   
2. Place each of the cars along a line running from the center to the outer edge of the board at approximately 6-inch intervals, as shown in
   Figure 15-1
   . (You can also do this with pennies or other objects instead of cars.)
   
3. Predict what you think will happen to the cars as you start to rotate the board around the pivot point.
   
4. Rotate the board, very slowly as first, but then pick up speed. What happens to the cars?
   

Cars furthest from the center begin to move first. As the cars start to move, they move away from the center, as shown in
Figure 15-2
.

The cars remain on the board as long as the frictional force is greater than the centripetal force needed to keep the cars moving in a circular path. The further you are from the center of rotation, more centripetal force is needed. For this reason, the cars furthest from the center are the first to move.

Figure 15-2
Cars further away from the center of rotation require more friction to remain stationary
.

This can also be done using pennies on a rotating surface, such as a turntable.

Friction can provide the centripetal force needed to keep an object moving along a circular path. If the force of friction is not sufficient to provide the centripetal force for a given radius, the object will depart from its circular path.