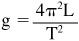125 Physics Projects for the Evil Genius (17 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

Typical human reaction time is about ¼ second. Most of the time, people are unable to catch the bill. Occasionally, someone can get lucky and anticipate the falling dollar. If you are offering to let the person keep the bill if they catch it, you may want to consider a smaller denomination.
The distance an object takes to fall is related to the time it takes to fall that distance. Knowing the time lets you predict the distance. Similarly, knowing the distance lets you predict the time.
Weightless water. Losing weight in an elevator
.
When things fall, they no longer
seem
to have weight. Objects, including people, float in the Space Shuttle as if there were no gravity. The shuttle orbit is not that high above the earth’s surface for the gravitational attraction to the Earth to disappear and, if the shuttle were not moving so rapidly in orbit, it would be pulled straight down to the earth. So, where does the force of gravity go to make the shuttle astronauts seem weightless? It has to do with the forces on falling objects. In this experiment, you investigate what happens to the weight of falling objects using a falling cup of water and by holding a weight on a scale in an elevator.
- cup with a few holes in it
- water
- spring scale
- mass
- optional: an elevator
- Fill the cup with water. Observe what happens.
- Drop the cup (over a sink or bucket). Observe what happens.
- Hang the mass on the spring scale.
- With the mass held stationary, note the weight of the object.
- While holding the scale, let the scale and mass drop toward the floor. Stop both just before they hit the floor.
- You don’t have much time to do this, but observe the scale reading as it first starts to fall and the reading as it is slowed prior to hitting the floor.
- Again, while holding the scale, raise the scale and mass from the floor. Bring it to a stop while you’re still holding it.
- If you can get to a real elevator, observe the scale reading with the mass suspended as the elevator goes up and as the elevator goes down. Even in a real elevator, you will find the period of acceleration for you to make these observations is short because elevators reach a steady velocity fairly quickly.
The water drips out from the holes when the cup is filled with water and held stationary. The water stops dripping when the cup is in free-fall.
The scale reads a greater weight when you lift the mass. With your arm fully extended as the scale and mass slows, the scale reads a lower reading than while stationary.
The scale reads a lower weight when you drop the mass. As you slow the scale and mass as it
nears the floor, the scale reads a higher reading than while stationary.
With the elevator, the scale reads a higher weight when it first starts to go up and a lower weight as the elevator slows to the next stop. Going down, the scale reads lower at first, and then higher at the next stop.

If the starting-up and slowing-down phase is uniformly spread over about 1 second, the change in apparent weight measured by the scale should change (very briefly) by not quite 50 percent. These changes are illustrated in the following
Figures 21-1
,
21-2
, and
21-3
.

Figure 21-1
Object at rest
.

Figure 21-2
Upward acceleration
.

Figure 21-3
Downward acceleration
.
With the cup held, the water is drawn through the openings by gravity. However, when the cup is in free-fall, it falls at the same rate as the water. While falling, the water is (apparently) “weightless,” similar to astronauts in the shuttle. If the cup wasn’t falling, the bottom of the cup would resist that pull, leaving the water no other resort than to fall out of the holes. However, with
the cup falling, the water does not experience a force from the cup opposing its downward movement. Because the cup was falling, the water in the cup seemed weightless.
We have all seen images of astronauts floating in the shuttle and space station, as if they were “weightless.” As a tube of scrambled eggs floats by an astronaut, it certainly appears that way. However,
weight
is the force caused by gravity on a mass and, although that attraction drops off as the inverse square root of the distance, it never becomes zero. In fact, at the shuttle orbit of 200 km, the force of the Earth’s gravitational attraction is only about 6 percent lower than what it is on the surface of the earth.
Objects in orbit are essentially falling at a speed consistent with maintaining the orbit. The apparent weightlessness of objects in space is the result of the objects in the shuttle falling to Earth at the same speed as the shuttle itself is falling. Because the water is falling at the same speed as our cup, it, too, appears weightless. When we hold the cup, we balance the force of gravity on the cup only, but not on the water. In that case, the water has weight that spills out of the holes in the cup.
The weight measured on the scale is a combination of the actual weight decreased or increased by the effect of accelerating the weight. It
does not matter how fast
the weight is moving. Once a high-speed elevator gets going at its cruising velocity, the measured weight should exactly equal the stationary weight. It is only the acceleration experience during the stopping and starting that affect the force on the object during that time.
A visual accelerometer can be used to indicate the direction and relative magnitude of the accelerations that accompany the weight changes encountered here.
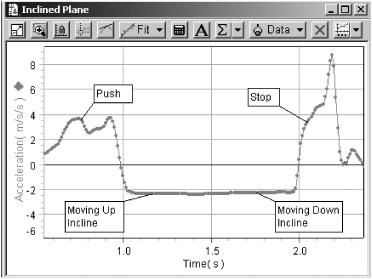
Figure 21-4
Courtesy PASCO
.
Using a motion sensor to measure an object moving up and then down an incline provides a closer look at the acceleration of an object subjected to gravity.
Figure 21-4
shows the acceleration versus time displayed in DataStudio. This shows that acceleration is downward (slightly more than −2 m/s
2
) for both the uphill and downhill segments of the graph.
The sensation of weight is caused by a force (such as the ground) holding you up. This upward (or normal) force, whether exerted from below (as in the cup) or above (as with the scale and weight), is how we experience weight. If the object supporting us is also falling, we are no longer exposed to the force we experience as weight.
What planet are we on? Using a swinging object to determine the gravitational acceleration
.
This project explores an indirect way of measuring the gravitational acceleration of the Earth (or any other planet you may do this experiment on). Because gravitational acceleration affects how fast a pendulum swings, we can take advantage of that to find the gravitational acceleration provided by measuring two things: how
long
the pendulum is and how much
time
it takes to swing back and forth. (If you are less than eighteen years old, please be sure to get your parents’ permission for any interplanetary travel for this project.)
- pendulum consisting of a mass supported by a string attached to a support
- pendulum with a long string and a large mass such as a bowling ball supported (safely and securely!) from the ceiling
- stopwatch
- Measure the period of a pendulum by measuring how long it takes for the pendulum mass to swing back and forth one time. Since this may be less than a second, more accurate measurements can be made by counting the time for 10 back-and-forth excursion, and then dividing by 10. Remember that in counting the cycles, the first cycle is counted when the mass returns to the point from which it was released and not at the point when it is first released.
- Measure the length of the pendulum. This is the distance in meters from the center of the hanging mass to the point of attachment.
- Try to minimize vibration of the ring stand or other support structure. Also keep the pendulum moving in two dimensions. Some people like to use a double string—one on either side of the mass—to keep the pendulum from wobbling.
- Calculate the gravitational acceleration,
g
(in meters per second per second), using the equation: