125 Physics Projects for the Evil Genius (16 page)

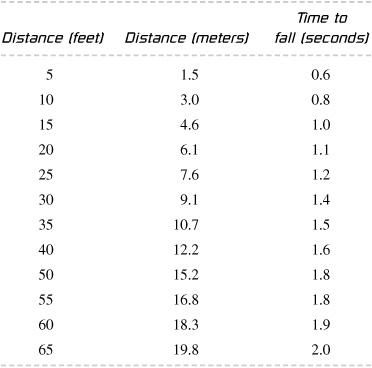
Another result expected is that, within the accuracy of this experiment, all objects fall at the same rate of acceleration, regardless of their mass.

Notice how sensitive the results are on the time measurement. For instance, suppose you drop a bowling ball from a 4.6 meter height and measure 1.1 seconds instead of 1.0 seconds. That 0.1 second error would result in a calculated value for gravitational acceleration of 7.6m/s
²
instead of the expected value of 9.8 m/s
²
or a 22 percent error. A 0.1 second error is less than the reaction time of most people so it is a good thing that we have another way to make this measurement.

With a motion sensor, the range of measurements is much tighter. The position versus time graph is shown in
Figure 19-3
. Notice this shows a curved line typical of acceleration. As the ball falls, the position increases, s the portion of the curve sloping up to the right represents the falling motion. After the ball bounces off the floor, the distance increases, which generates the curved line that slopes down to the right. This graph shows an initial release and then two bounces. The data collection stops just before a third bounce.

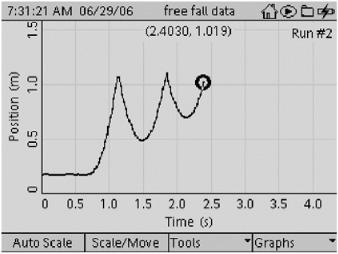
Figure 19-3
Position versus time for a falling ball showing two full bounces. Courtesy PASCO
.

A velocity versus time graph generated by a motion sensor is shown in
Figure 19-4
. Gravitational acceleration is given directly by the slope of the line. This can be determined by dividing the rise (change in velocity) by the run (corresponding change in time). The slope can also be found by using the slope tool located in the DataStudio pull-down menu. This graph shows the same drop followed by two bounces, as you saw in
Figure 19-3
. Notice the first bounce occurs just before 1.2 seconds. The ball reaches its first peak at 1.5 seconds and begins to fall again. In
Figure 19-4
, the velocity rapidly changes from positive (above the line) to negative (below the line).

Also notice one interesting aspect of the physics of free-fall, illustrated by
Figure 19-4
. After each bounce, the slope is the same
below
the zero line (bouncing up), at the zero line (at the highest point) and
above
the zero line (falling back down). What this means is gravitational acceleration is
constant
and affects an object in free-fall,
regardless of whether it is moving up or down
.

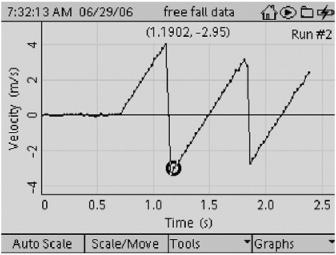
Figure 19-4
Velocity versus time for a falling ball. The slope of each line gives the acceleration of the ball in free fall. Courtesy PASCO
.

Part 1
is a direct measurement and application of the basic motion formula:

a = 2d/t
²

where we find the acceleration due to the force of gravity.

Part 2
measures the same thing, but it uses a much more precise measurement of the distance traveled in a given time. We know from
Projects 1
and
2
that the slope of the distance versus the time graph gives a measure of velocity. Similarly, the slope of the velocity versus the time graph gives acceleration. Each bounce provides a replication of this experiment that can provide a separate data point.

A motion sensor reveals the brief time that a ball encounters the ground as it compresses, decompresses, and eventually reverses direction. Some balls do this more quickly than others. This can be seen in time-lapse photography but can also be noticeable in the distance versus time graphs generated by motion sensor.

There is another method for measuring the Earth’s gravitational acceleration using a pendulum. See
Project 22
. Compare this with the results you get with the motion sensor.

This experiment gives two ways to measure the acceleration on any object caused by the gravitational force of the Earth. The first way is a direct measurement limited by the reaction time to record how long it takes an object to fall. The second method uses a motion sensor that captures this data with greater resolution and precision, and when interpreted graphically gives a more accurate value for gravitational acceleration. In either case, the correct value is 9.8 m/s
²
or 32 ft/s
²
.

This experiment explores the nature of
free-fall
: the longer an object falls, the greater the
distance
it falls. Measuring the distance an object falls can give an indication of the
time
. This can be used to estimate a person’s reaction time. You use both a dollar bill and a meterstick to prove this point.

• meterstick
  

1. This requires two people. The first person holds a meterstick upside down, so the end that reads 0 cm is directed downward.
   
2. The second person holds their fingers at the bottom of the meterstick ready to grab the meterstick, as shown in
   Figure 20-1
   .
   
3. The meterstick is dropped, and then caught as shown in
   Figure 20-2
   .
   
4. The
   distance
   the meterstick falls is an indication of the person’s reaction
   time
   . Under gravitational acceleration, distance is related to time according to the equation d = ½ gt
   ²
   where
   g
   is the gravitational acceleration constant, 9.8 m/s
   ²
   , and time is measured in seconds. This equation gives the distance in meters. This relationship is tabulated in
   Table 20-1
   :
   

Figure 20-1
Ready to catch the meterstick
.

Figure 20-2
The position where the meterstick is caught is an indication of the time it was falling
.

Table 20-1

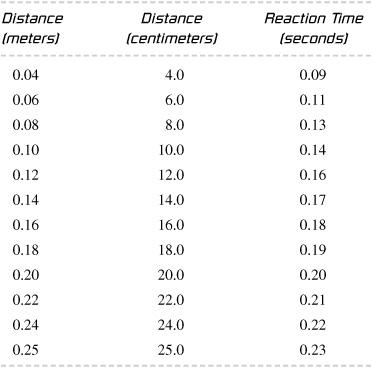
The reaction
time
can be determined by the
distance
that the meterstick falls before being caught. The meterstick will typically fall about 10–20 centimeters before being caught, but this will vary with the individual.

The distance an object falls increases with the
square
of the time it falls. Similarly, the time it takes to fall is proportional to the
square
root of the distance.

A dollar bill is about 15.2 cm (6 inches) in length. According to the previous chart, it will take a dollar bill nearly 0.18 seconds to fall. Challenge someone to catch the dollar. Unless the person anticipates that release, the bill will fall (almost every time).

Figure 20-3
Money often seems to fall through our hands. It falls through its own length in a time less than most people’s reaction time
.