125 Physics Projects for the Evil Genius (18 page)

where
L
is string length in meters and
T
is time in seconds. (This will also work if you measure
L
in feet but you will get an answer in feet per second per second.) Try this multiple times and take the average to get the most accurate result. See
Figure 22-1
.

Gravitational acceleration should be close to the accepted value of 9.81 m/s
²
. Results within 2 percent of this value are easily achievable. If you are working with feet, gravitational acceleration is 32 feet/s
²
. Longer pendulum lengths encounter less frictional loss and are easier to get an accurate period measurement. Remember, 100 centimeters is equal to 1 meter when determining the length of the pendulum.

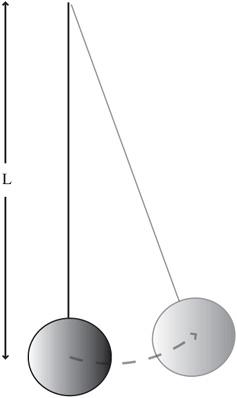
Figure 22-1
Using a pendulum to find
g.

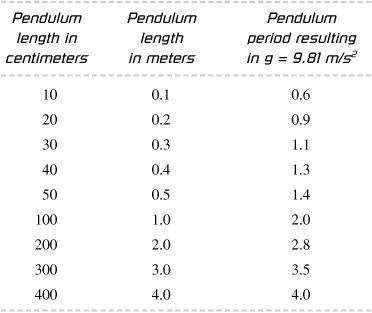
The following set of values results in the 9.81 m/s
²
target value for gravitational acceleration:

It stands to reason that the greater the pull of gravity, the faster the pendulum motion and the shorter the period. This is given by the equation for the period of a pendulum:

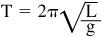
where
L
is the length (in meters) and the period is one cycle back and forth (in seconds). Solving this for gravitational acceleration gives us:

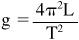
The definition of the period of a pendulum is the number of seconds for it to swing
back and forth
one time.

You have been captured by alien abductors and taken to an unknown planet (where there are no video games and no cable TV). You are able to remove your shoe, which has a 15 cm (0.15 m) shoelace. You find that when you let your shoe swing freely in a short arc, it returns to the point from which it was released in 1.26 seconds. To which planet should you direct the interplanetary rescue team? The gravitational acceleration on the various planets is: Venus 8.93 m/s
²
, Earth 9.81 m/s
²
, Mars 3.73 m/s
²
, Jupiter 924.9 m/s
²
, and Saturn 10.6 m/s
²
. Try it. (Hint: the answer is this planet is one of Earth’s neighbors in space possessing a very thin atmosphere, ice caps, and a reddish clay-like surface.)

For a given string length, the period of the pendulum depends on the gravitational acceleration. This provides a fairly accurate method for measuring the local gravitational acceleration.

An object at rest (including an object at rest on top of a tablecloth) tends to stay at rest unless acted on by an external force. One way to prove this is to pull a cloth out from under the object. This can be done more simply at first or more elaborately as you build your confidence in the law of physics.

• tablecloth (one with low friction is best—tweedy fabrics, gravy spots, and spilled soda can increase friction and compromise the intended results)
  
• table
  
• objects to place on the tablecloth such as bowls, bottles, lit candles, and your physics textbook
  
• spare roast turkey, stuffing, and cranberry sauce, if you actually attempt to do this at
  your
  Thanksgiving dinner
  

1. Place the cloth on the table, so at least several inches extend beyond the edge of the table.

2. Carefully place the objects on the cloth. If the objects are closer to the edge of the table this is easier, but allow for at least a few inches for the objects to slide.

Figure 23-1
Don’t hesitate!

3. At this point, all you need to do is pull the tablecloth out from under the objects on the table. As with a band-aid,
the faster the better
. Don’t hesitate and be tentative with your pull because that increases the chances for the objects to topple. (It doesn’t hurt to create suspense by pretending you never did this before and have every reason to expect it to fail. The more you do this, the greater level of acting skills this may require.)

Figure 23-2
A fast pull works better than a tentative pull
.

4. You can also do this with just one beaker and a cloth. Perhaps this is a less-dramatic start, but it still proves the same point.

Note: This works best when objects placed on the tablecloth have smooth bottom surfaces. Bowls with a circular lip tend to catch on the tablecloth. Pottery with a felt bottom or mounted silicon rubber resting points can also lead to humiliation and ridicule if they hang up during this demonstration. The objects should have a short vertical “moment arm,” which means bowls are safer than bottles and partially filled bottles are safer than empty bottles. Bottles with liquid should be at room temperature to avoid condensation on the outside of the bottle, which can increase friction.

The cloth is removed and the objects-at-rest sitting on the tablecloth tend to stay at rest in approximately the same position they were originally placed. Most likely, there will be some sliding and even teetering before the objects come to rest.

The criterion for stability is that the height to diameter ratio for cylindrical objects be less than the coefficient of static friction between the cloth and the object.

This is basically a fun experiment, but there is a good bit of physics to learn here. The objects retain their positions on the table due to
Newton’s first law
, which states that an object in motion tends to stay in motion unless acted upon by an external force. (An object at rest tends to stay at rest
unless acted upon by an external force
.) If excessive friction exists between the cloth and the bottom of the objects, there will be an external force and the objects will move. The table must have low enough friction so the tablecloth can be pulled out smoothly, but enough friction so the objects don’t slide too far after the cloth is removed. The small frictional force that occurs when the cloth is pulled out exerts a torque that can rotate the object, especially one whose center of mass is relatively high above the table. The frictional force exerted by the table on the bottom surface of the objects opposes this rotational motion and helps stabilize tall objects, such as bottles and candlesticks.

As a way to get in touch with your inner nerd, you can draw diagrams, called
free-body-diagrams
, showing all the forces present in this project. You can learn a lot of physics by doing this.

One aspect of Newton’s first law is that an object at rest tends to stay at rest. This can be seen in the reluctance of the objects on the table to be moved as the cloth is pulled out from under them. Some frictional force exists between the cloth and the objects, which exerts a torque that, if strong enough, will rotate and topple the object.

This experiment further explores Newton’s first law in both the horizontal and vertical directions.

• 5 to 10 poker chips (or coins)
  
• table
  
• string—strong enough to support the mass, but weak enough to break when pulled
  
• 1 weight with attachment points on both the top and bottom
  
• 1 support to hang the weight