125 Physics Projects for the Evil Genius (20 page)

Figure 25-4
Acceleration as a function of the hanging mass. Courtesy PASCO
.

Newton’s second law, which states that F = ma, or as Newton originally put it, a = F/m.

• m
  represents the
  entire mass
  of the system and includes the
  mass of the cart (m
  _c
  ), plus the mass in the cart (m
  ₁
  ) plus the hanging mass (m
  ₂
  )
  .
  
• F
  is the applied force that pulls the cart and is given by the hanging mass, m
  ₂
  (in
  kilograms
  , not in grams) times the gravitational acceleration (9.8 m/s
  ²
  ). (To get kilograms from grams, divide the number of grams by 1000.)
  
• a
  is the acceleration (in m/s
  ²
  ) of the
  entire system
  , including the cart, its contents, and the hanging mass.
  

You can use the following to organize your data:

For a fixed mass in the cart (m
₁
), the greater the applied force, the greater the acceleration. The expected relationship between acceleration and force is shown in
Figure 25-4
, which (for simplicity) shows the effect of increasing the hanging mass on acceleration. (The actual driving force is given in newtons, which is simply 9.8 times the mass in kilograms.) Without friction (and to the extent that friction is eliminated from this experiment), this should be a linear relationship as indicated in
Figure 25-5
.

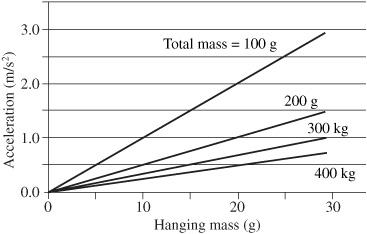
Figure 25-5
Predicted acceleration versus applied force for different values of (total) mass
.

For a given applied force, the heavier the load, the smaller the rate of acceleration. This is an
inverse
relationship, as shown in
Figure 25-6
.

Experimental results for acceleration for a given mass and applied force come close to the predicted results if the frictional forces are not significant. Even with friction, it can still be shown that acceleration depends on applied force and is inversely proportional to the mass. Friction increases when too much mass is placed in the cart. However, if the mass is too small, the acceleration can be so high, it becomes more difficult to measure accurately.

Use of low-friction tracks reduces the amount of friction. Motion sensors provide a nice way to determine the acceleration.
Figure 25-7
shows the result of motion sensor data for two different total accelerated masses.

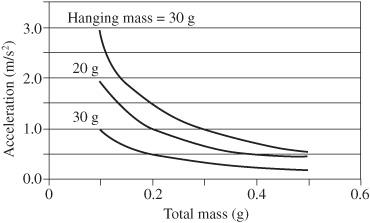
Figure 25-6
Predicted acceleration versus total mass
.

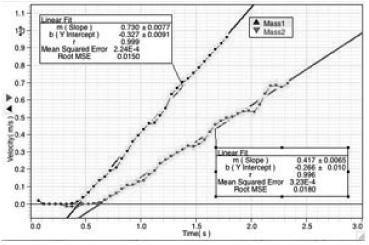
Figure 25-7
Velocity versus time for two different masses accelerated by a constant force. The slope of the v-t curve gives the acceleration. Courtesy PASCO
.

Newton’s second law states that F = ma or a = F/m. More force leads to greater acceleration, but more mass lowers the rate of acceleration.

You may want to consider doing this using a Hover Puck drawn across the floor by a mass hung from a pulley, as shown in
Figure 25-8
. As before, remember to include the mass of the Hover Puck as part of the total system mass being accelerated. The higher the pulley is supported above the floor, the longer the run you can have across the floor. A qualitative but very intuitive way of showing the relationship between a force and acceleration can be shown using an LED accelerometer. The constant force from the fan results in an acceleration indicated by the LEDs as shown in
Figure 25.9
. The direction of the force vector is in the same direction as the acceleration vector.

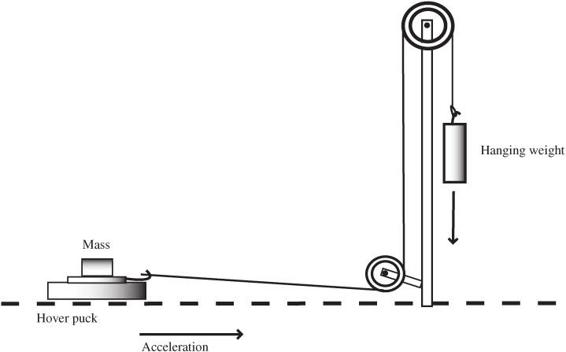
Figure 25-8
Using a Hover Puck to prove Newton’s second law
.

Figure 25.9
The fan exerts a force which accelerates the cart. The LEDs on the accelerometer show how the cart accelerates. Courtesy PASCO
.

The result here is one of the most significant results in physics: a force causes acceleration. For a given mass, the acceleration of an object is proportional to the applied force. For a given force, the acceleration is inversely proportional to the amount of mass.

If Sir Isaac Newton had a skateboard, it might have saved him some time in discovering his third law, although Newton might have had so much fun doing it, he wouldn’t have had time to invent calculus. The laws of physics apply to all objects. Sports, in particular, can be thought of as intuitive applications of the principles of physics. This experiment takes advantage of the fact that all objects in the universe follow the laws of physics. We focus particularly on Newton’s third law and conservation of linear momentum.

• 2 rolling chairs
  
• or 2 people capable of keeping their balance on skateboards (each with helmets); rollerblades will also work
  
• medicine ball or a several pound mass, such as a bowling ball
  
• safe place to do this
  

1. Two people face each other sitting in the chairs on rollers, a few feet apart.
   
2. One person tosses the medicine ball to the other (both are seated in chairs). Feet should be kept off the floor, so the chairs are free to move.
   
3. The two people again face each other. One tries to push the other. What happens?
   

The person who catches the ball, as well as the person who throws the ball, will move backward. Similarly, the person doing the pushing, as well as the person getting pushed, will recoil backwards.

Momentum is mass times velocity.

At the start of this, the two skateboarders have zero momentum (they have mass, but no velocity, so their momentum is zero).

The velocity of the ball transfers momentum from the first to the second person. The first person recoils backward. The second person also moves backward in the opposite direction.

Another principle illustrated here is Newton’s third law: For every action (movement of the ball), there is an equal and opposite reaction (recoil of the person in the chair).

The previous demonstrations can be done by skateboarders or rollerbladers. (Please remember, although we are interested in horizontal action and reaction here, gravity is still active in the vertical direction, so keep your balance.)

Conservation of linear momentum and Newton’s third law can be demonstrated by attaching a
mousetrap to a low-friction cart. The trap is set and a tennis ball is positioned in place of the cheese. When the mousetrap is released, the process of tossing the ball results in the equal and opposite reaction of the mousetrap recoiling in a backward motion. This is shown in
Figure 26-1
. Both the mousetrap and the ball initially have zero momentum. The momentum of the ball going to the left is equal but opposite to the momentum of the mousetrap and cart moving to the right.