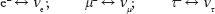Beyond the God Particle (51 page)

2
. Heisenberg's uncertainty principle: The uncertainty principle implies that if we try to localize any particle in space within a very small region of distance, Δ
x
, the uncertainty in position, then the uncertainty in the
x
-component of the momentum of the particle, Δ
p
_x
, will grow larger, becoming at least as big as Δ
p
_x
≥ h/2πx
. Similarly, if we want to localize some event in a system within a tiny time interval, Δ
t
, then we will necessarily disturb the system and cause a range in its energy of Δ
E
, where Δ
E
Δ
t ≥ h
/2
π
, so the smaller we make Δ
t
, the larger becomes Δ
E
, as Δ
E ≥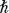
/Δ
t
. The atomic orbitals of electrons have a typical size in most atoms of roughly Δ
x
≈ 10
^–10
meters in any given direction in space. Therefore, electrons must, by the uncertainty principle, have a range of momentum within their orbitals that is as large as Δ
p
_x
≥
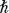/Δx
, hence, Δ
p
_x
≈ 10
^–24
kilogram-meter/second. Electrons move in their orbitals with velocities that are much less than
c
(i.e., they are
non-relativistic
), and the electron mass is known to be
m
_e
≈ 9.1 × 10
^–31
kilograms. Therefore, we can estimate the typical electron kinetic energies to be of order,
E
≈ (Δ
p
_x
)/2
m
_e
≈ 6 × 10
^–19
joules, or about 3.8 electron volts (1 electron volt = 1.6 × 10
^–19
joules; we have done a lot of “rounding off” to do this “back-of-the-envelope” estimate). The force that holds the electrons in their orbitals must therefore provide a negative potential energy that exceeds, in magnitude, this result. This is the electromagnetic force, and the typical scale of the
binding energies
of electrons in an atom (the energy we must supply to liberate them) is of this order, ranging over about 0.1 to 10 electron volts. In fact, this is the typical energy scale of all chemical processes, and it contains the typical energies of visible light photons.

A “quantum fluctuation” is a bit like a “thermal fluctuation.” It is physically possible for a thermal system, like a hot gas in a room, to suddenly fluctuate in density and pressure—even the extreme fluctuation of all of the gas momentarily condensing onto the floor then evaporating back into the room is physically possible, but such a thing is ultra-ultra rare. Note that a top quark is heavy enough that the top can directly decay, converting to a b-quark and a W
⁺
, without requiring the uncertainty principle.

3
. In any physical process, when a direction in space (called a vector) becomes correlated with a spin or a magnetic field (which is a “pseudovector”; the mirror image of a pseudovector is opposite that of a vector), then there is parity violation, since in the looking-glass house the correlation would be opposite; i.e., for Leon's experiment, in the looking-glass house the electrons would come out in the opposite direction of the muon spin. In Madame Wu's version of the experiment, the electrons coming out of
⁶⁰
Co decay were aligned with the direction of the magnetic field used to align the spins of the nuclei.

4
. The relationship is simple math, if you have had calculus: the electric and magnetic fields are the particular derivatives of the gauge field in space and time.

5
. Sheldon Glashow, “Partial Symmetries of the Weak Interactions,”
Nuclear Physics
22 (1961): 579–88.

6
. Steven Weinberg, “A Model of Leptons,”
Physical Review Letters
19 (1967): 1264–66.

7
. Gerard ‘t Hooft and Martinus Veltman, “Regularization and Renormalization of Gauge Fields,”
Nuclear Physics
B44 (1972): 189–213.

8
. In particular, fermions are spin-1/2, or “half-integer” spins. See Leon M. Lederman and Christopher T. Hill,
Quantum Physics for Poets
(Amherst, NY: Prometheus Books, 2011) or the discussion of spin in the Appendix.

9
. See “Satyendra Nath Bose,”
http://en.wikipedia.org/wiki/Satyendra_Nath_Bose
(site last visited 1/23/2013).

10
. This is a complicated phenomenon that involves the interactions of the electrons in the atoms—for most magnetic materials the atoms align but cancel the overall field to zero. Iron prefers a ground state in which there is an exact common alignment, and we get a big magnetic field emanating from the iron.

CHAPTER 7. MICROSCOPES TO PARTICLE ACCELERATORS

1
. This news bulletin was from CNN Tech:
http://articles.cnn.com/2009-11-21/tech/cern.hadron.collider_1_large-hadron-collider-lhc-cern?_s=PM:TECH
(site last visited 1/23/2013).

2
. Some early history of microscopes can be found here:
http://en.wikipedia.org/wiki/History_of_optics
;
http://en.wikipedia.org/wiki/Magnifying_glass
;
http://www.history-of-the-microscope.org/
(sites last visited 6/21/2013).

3
. See “Zacharias Jannsen” and references therein,
http://en.wikipedia.org/wiki/Sacharias_Jansen
; “History of the Microscope”
http://www.history-of-the-microscope.org/hans-and-zacharias-jansen-microscope-history.php
(sites last visited 1/23/2013).

4
. Miscellaneous references on the history of microscopes:
http://inventors.about.com/od/mstartinventions/a/microscope.htm
(site last visited 1/23/2013); R. M. Allen,
The Microscope
(New York: D. Van Nostrand Company, Inc., 1940);
The
S. Bradbury,
Evolution of the Microscope
(Oxford: Pergamon Press, 1967); W. G. Hartly,
The Light Microscope
(Oxford: Senecio Publishing Company, 1993). See also “Telescope,”
http://en.wikipedia.org/wiki/Telescope
; Henry C. King and Harold Spencer Jones,
The History of the Telescope
(Courier Dover Publications, 2003).

5
. See “Antonie van Leeuwenhoek,”
http://en.wikipedia.org/wiki/Van_Leeuwenhoek
(site last visited 1/23/2013); Alma Smith Payne,
The Cleere Observer: A Biography of Antoni van Leeuwenhoek
(London: Macmillan, 1970).

6
. Anton van Leeuwenhoek, Letter of June 12, 1716. The letter and short biography can be found here:
http://www.ucmp.berkeley.edu/history/leeuwenhoek.html
(site last visited 1/23/2013).

7
. See “Robert Hooke” and references therein,
http://en.wikipedia.org/wiki/Robert_Hooke
(last visited 1/23/2013).

8
. A beam of light bends as it obliquely hits water or glass. This bending of light by transparent materials is called refraction. The amount of refraction is controlled by the “index of refraction” of the medium the light is exiting (e.g., air) and that the light is entering. The index of refraction varies with light wavelength. This is the basis of the phenomenon of a glass prism that splits the white light into its spectral constituents: Red-Orange-Yellow-Green-Blue-Indigo-Violet (ROY G. BIV). White light is therefore composed of equal amounts of the different colors of light. We can take the colors of light and combine them to make white light. The chromatic aberration is mainly the prism effect of the glass lens.

9
. See “Joseph Jackson Lister,”
http://en.wikipedia.org/wiki/Joseph_Jackson_Lister
; see also “Lens,” under “Optics” heading,”
http://en.wikipedia.org/wiki/Lens
(sites last visited 1/23/2013). Lister published his work in 1830 in a paper titled “On Some Properties in Achromatic Object-Glasses Applicable to the Improvement of the Microscope,” submitted to the Royal Society.

10
. Lenses and aberrations are thoroughly discussed here:
http://en.wikipedia.org/wiki/Lens_%28optics%29#Compound_lenses
, and here:
http://en.wikipedia.org/wiki/Compound_lens
(sites last visited 4/10/2013).

11
. D. Edwards and M. Syphers explain this and much of optics with some simple matrix algebra in an elegant book:
An Introduction to the Physics of High Energy Accelerators (Wiley Series in Beam Physics and Accelerator Technology)
(Wiley, 1992), pp. 60–65.

12
. Let's review the physics of a wave: Consider a long traveling wave as it moves through space. We can visualize this as a freight train moving by as we are stopped at a railroad crossing. A traveling wave is sometimes called a wave train, with many sequential crests and troughs of the train as it traverses space. Such a wave is described by three quantities: its frequency, its wavelength, and its amplitude. The wavelength is the distance between two neighboring troughs or crests of the wave. The frequency is the number of times per second the wave undulates up and down through complete cycles at any fixed point in space. If we think of the wave as a long freight train, its wavelength is then the length of a boxcar. Its frequency is the number of box cars per second passing in front of us as we patiently wait for the train to pass. The speed of the traveling wave is therefore the length of a boxcar divided by the time it takes to pass, or (speed of wave) = (wavelength) times (frequency). Thus, knowing the speed, the wavelength and frequency are inversely related, or (wavelength) = (speed of wave) divided by (frequency) and (frequency) = (speed of wave) divided by (wavelength). The amplitude of the wave is the height of the crests, or the depth of the troughs, measured from the average. That is, the distance from the top of a crest to the bottom of a trough is twice the amplitude of the wave, and it can be thought of as the height of the boxcars. For an electromagnetic wave, the amplitude is the strength of the electric field in the wave. For a water wave, twice the amplitude is the distance that a boat is lifted from the trough to the crest as the wave passes by.
Figure 2.1
says it all. The color of a visible light wave was understood in the nineteenth-century Maxwellian theory of electromagnetism to be determined by the wavelength (and, inversely, the by frequency). If we take the frequency to be small, we correspondingly find that the wavelength becomes large. Longer-wavelength visible light is red, while shorter-wavelength visible light is blue. For graphic display in color of the various wavelengths of light, see
http://science-edu.larc.nasa.gov/EDDOCS/Wavelengths_for_Colors.html#blue
(site last visited 3/26/2013).