Brain Trust (24 page)

Oh, I forgot the added bonus: If you figure out how to find the shortest route, the Clay Mathematics Institute will give you a million dollars. That’s because, to date, no one has provided a general solution (or proven a solution’s impossible) to this type of problem—called “the traveling salesman”—in which you have to minimize total distance traveled among many points.

It has many applications: Imagine you’re standing in the middle of a court littered with tennis balls. What’s the shortest distance you can walk to pick them all up? Or how can you see all the major landmarks of Paris in an afternoon?

The problem is that, “as the number of stops grows toward infinity, so too does the number of possible routes,” says William Cook, mathematician at Georgia Tech. At some point, the magnitude of possible choices simply overpowers computational resources. So Cook takes a novel approach. Instead of using brute force computation to search through the haystack of nearing-infinite routes for the best solution, Cook explores sufficing—how can you
nearly
find the shortest tour between errands, and once you have a candidate, how can you know how good or not good it is? Cook says, “If I give you a ten-mile tour, you might be
unsatisfied, unless I can guarantee with some degree of certainty that there are no shorter tours.”

This allows us to start our errands without having to wait the many generations the Deep Thought supercomputer might take to discover the optimal route of forty-two miles (and if you get this reference, I imagine you’ll find many little chuckles throughout this book).

So how should you suffice? “If every time you go to the nearest place you haven’t yet visited, it gets you within 25 percent of the shortest tour,” says Cook. What errand is closest to you? Go there. And then look around again—now which one’s closest? Continue until you’ve visited each stop, and you’re mathematically certain to be within 25 percent of the shortest route. (Remember to think time and not distance when computing “nearest.”)

Once you’re cool with that, here’s a nice refinement: Draw your tour, always going to the closest place not yet visited, and then look for places where the route intersects itself. Uncross any crosses. (This makes no sense until you draw it, like on the next page, and then it’s obvious). This gets you within 10 percent of the optimal tour. If you can solve the tour completely, the Clay Institute has a million bucks for you.

The traveling salesman problem is a clean
illustration of applied versus pure mathematics. Cook has solved optimal tours up to 33,810 stops and tours within 1 percent of optimal are available for millions of stops. But that’s not a solution. To date, there exists no general procedure for finding the optimal route among × number of stops.

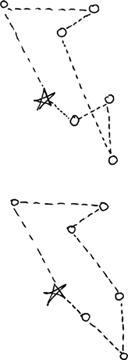
Puzzle #13:
A Three-Hour Tour?

Draw the shortest tour starting and ending at the house, and touching all the points in the picture below.

Let’s imagine Armageddon comes not in the form of a mighty asteroid that obliterates the planet, or as nuclear winter that blocks the sun and drives all life far underground for ten uranium half-lives, or as a Norwegian wolf that breaks free of its underworld restraints to consume the gods, but as something gentler like complete infrastructure collapse or an abrupt end to fossil fuel supplies.

In that case, even after the grocery stores are looted, you can survive without food for at least a month and maybe much longer (thank you, obesity epidemic!), but you need water within an absolute maximum of ten days or you’re a goner. And in most areas, ensuring an adequate yearly supply of drinkable water is no easy feat (thank you, marmots peeing in even the clearest-looking mountain streams!). Simply, if you can’t trap and treat your own water, you’re toast.

One option is to use roofs. “Rainwater harvesting and catchment off roofs isn’t new,” says Mira Olson, civil engineer at Drexel University. The Byzantines did it residentially and the Romans did it industrially. First, tin or terra-cotta roofs are good, asphalt and shingles are bad, as is “proximity to birds,” says Olson (the last due to the same reason you don’t park your car beneath a roost). Also, in the first rain after a dry spell, let the first water run off the roof before connecting your system—this first flush will take with it the majority of contaminants.

But the neat part is in treatment methods. When you run out of chlorine tablets, throw in a crab shell. The shell’s chitosan binds organic contaminants like bacteria, algae, and even that stray bit of marmot pee. As long as you don’t eat the chunks of shell, you should be fine.

Or, “If you can filter water through a clear tube, the sunlight
inactivates the bacteria for you,” says Olson. Rather than killing bacteria, UV light fries bacterial DNA, making them unable to viably reproduce. You’ll drink the few first bacteria, but they’ll be unable to bloom in your gut. In fact, UV sterilization “pens” are available now for hiking and camping use, but forcing your harvested water to spend two to four hours percolating slowly through a clear tube in direct sunlight does the trick too.

The reward for this knowledge is the ultimate evolutionary prize: the right to repopulate the earth.

Mira Olsen works with Engineers Without
Borders to design catchment and other water systems that can be used and maintained sustainably by third world populations. In its own way, third world engineering is very
Mad Max
.

In 1972 Tony Alva jumped a fence to covertly skate a dry pool near California’s Venice Beach neighborhood. Soon, a core group of Venice surfers-turned-skaters, including Stacy Peralta, made pool poaching a habit. When the police came, they ran. But now in the recessed pools of skate parks around the country, kids have made Alva’s once innovative moves the norm. You know the story of
Dogtown and Z-Boys
. But how did Alva pull it off? How did this illegal, harebrained stunt become the social norm?

And how can you make your own harebrained ideas socially acceptable?

Simon Levin, evolutionary biologist at Princeton, explored the question from a slightly different angle: “In bird flocks and fish schools, you have a few individuals who think they know where they want to go, and the vast majority of individuals who are imitating,” he says. Levin builds software models of these schools with his collaborator, Iain Couzin. Basically, he tags individuals as leaders or followers (or percentages thereof), connects them to others in the school, and then flips the switch on individual fish to see how the change propagates through the group. By tweaking the model until it acts like a natural school of fish, he discovers the mechanisms that allow change to flow through groups. It’s like setting up a very detailed crowd of dominoes—when you knock one brick, how far and how fast does the ripple travel?

Or, that’s what Levin used to do.

Now he applies the mathematics of fish changing directions to groups of people changing opinions.

“First, social change relies on distributed networks,” says Levin. The opposite of “distributed” is a “well-mixed” network like that of a country with an authoritative central government, in which top-down control quickly suppresses novel opinions—nails that stick up are pounded down. “These systems are robust over short periods of time,” says Levin. But when top-down control fails, the whole system is shot.

Now imagine Venice Beach in the 1970s. In this far-flung node of a distributed network, when Alva had the idea to skate a dry swimming pool, the sheriff wasn’t able to kill it before it grew. These distributed networks, with pods of far-flung autonomy and an absence of top-down control, “have the capability for novel opinions and attitudes to spring up,” says Levin.

So if you want to change cultural norms, you need to live in a place where the seed of your idea can take root without being
summarily hit with Roundup by authority or the power of strong social norms. Perhaps innovating from a home base in Berkeley is easier than creating the same shift while based in Salt Lake City.

And the idea thus rooted can take over a population the same way a school of fish changes direction. “Individual fish or birds are attuned to the seven to ten fish or birds around them,” says Levin, “thus the first to imitate a behavior are those most similar to the individual in which the behavior arises.”

In the case of skating dry pools, these similar individuals were Alva’s neighborhood friends, who coalesced into the Z-Boys, defining themselves based on this new skate culture. And just like closely following a leading fish’s tight turn keeps following fish in the relatively safe center of the school, group members who quickly conformed to the new skateboard norms earned benefits. The Z-Boys had turf, they got girls, they were cool.

But in order for your innovation to spread beyond your posse, you need another important network feature: connectivity. The Z-Boys earned this connectivity at the 1975 Del Mar Nationals, where the pod of long-haired, Vans-wearing ne’er-do-wells rocked the socks off the clean-cut competition. The newly reformed
Skateboarding
magazine wrote a series of articles on Dogtown, and suddenly the Z-Boys had direct domino connection to kids across the country who wanted a piece of the action. The dominoes fell, and social norms changed course.

Levin points out the same progression of innovate-coalesce-connect in neckties, disallowing smoking in public places, tattoos, fingernail polish, gender equality, and recent rapid changes in the caste system of India. Today, you don’t wear a tie because it’s comfortable, but because it signals your membership in a group of professionals. What started as an affectation of Croatian mercenaries and earned fashion connectivity in Paris is now the social norm.

If you want to drive social norms, start by jumping a fence—any fence. Then push the idea on the seven to ten fish closest to you (see this book’s entry with Eli Berman about creating a posse of obedient henchmen). Then connect your dominoes to the world at large.

Puzzle #14:
Schooled by Fish