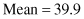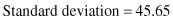Data Mining (11 page)
Authors: Mehmed Kantardzic

While some data-mining problems are characterized by a single time series, hybrid applications are more frequent in real-world problems, having both time series and features that are not dependent on time. In these cases, standard procedures for time-dependent transformation and summarization of attributes are performed. High dimensions of data generated during these transformations can be reduced through the next phase of a data-mining process: data reduction.
Some data sets do not include a time component explicitly, but the entire analysis is performed in the time domain (typically based on several dates that are attributes of described entities). One very important class of data belonging to this type is
survival data
. Survival data are data concerning how long it takes for a particular event to happen. In many medical applications, the event is the death of a patient, and therefore we analyze the patient’s survival time. In industrial applications, the event is often the failure of a component in a machine. Thus, the output in these sorts of problems is the survival time. The inputs are the patient’s records in medical applications and characteristics of the machine component in industrial applications. There are two main characteristics of survival data that make them different from the data in other data-mining problems. The first characteristic is called
censoring
. In many studies, the event has not happened by the end of the study period. So, for some patients in a medical trial, we may know that the patient was still alive after 5 years, but do not know when the patient died. This sort of observation would be called a censored observation. If the output is censored, we do not know the value of the output, but we do have some information about it. The second characteristic of survival data is that the input values are
time-dependent
. Since collecting data entails waiting until the event happens, it is possible for the inputs to change its value during the waiting period. If a patient stops smoking or starts with a new drug during the study, it is important to know what data to include into the study and how to represent these changes in time. Data-mining analysis for these types of problems concentrates on the survivor function or the hazard function. The survivor function is the probability of the survival time being greater than the time t. The hazard function indicates how likely a failure (of the industrial component) is at time t, given that a failure has not occurred before time t.
2.6 OUTLIER ANALYSIS
Very often in large data sets, there exist samples that do not comply with the general behavior of the data model. Such samples, which are significantly different or inconsistent with the remaining set of data, are called outliers. Outliers can be caused by measurement error, or they may be the result of inherent data variability. If, for example, the display of a person’s age in the database is −1, the value is obviously not correct, and the error could have been caused by a default setting of the field “unrecorded age” in the computer program. On the other hand, if in the database the number of children for one person is 25, this datum is unusual and has to be checked. The value could be a typographical error, or it could be correct and represent real variability for the given attribute.
Many data-mining algorithms try to minimize the influence of outliers on the final model, or to eliminate them in the preprocessing phases. Outlier detection methodologies have been used to detect and, where appropriate, remove anomalous observations from data. Outliers arise due to mechanical faults, changes in system behavior, fraudulent behavior, human error, instrument error, or simply through natural deviations in populations. Their detection can identify system faults and fraud before they escalate with potentially catastrophic consequences. The literature describes the field with various names, including outlier detection, novelty detection, anomaly detection, noise detection, deviation detection, or exception mining. Efficient detection of such outliers reduces the risk of making poor decisions based on erroneous data, and aids in identifying, preventing, and repairing the effects of malicious or faulty behavior. Additionally, many data-mining techniques may not work well in the presence of outliers. Outliers may introduce skewed distributions or complexity into models of the data, which may make it difficult, if not impossible, to fit an accurate model to the data in a computationally feasible manner.
The data-mining analyst has to be very careful in the automatic elimination of outliers because if the data are correct, that could result in the loss of important hidden information. Some data-mining applications are focused on outlier detection, and it is the essential result of a data analysis. The process consists of two main steps: (1) Build a profile of the “normal” behavior, and (2) use the “normal” profile to detect outliers. The profile can be patterns or summary statistics for the overall population. The assumption is that there are considerably more “normal” observations than “abnormal”—outliers/anomalies in the data. For example, when detecting fraudulent credit card transactions at a bank, the outliers are typical examples that may indicate fraudulent activity, and the entire data-mining process is concentrated on their detection. But, in many of the other data-mining applications, especially if they are supported with large data sets, outliers are not very useful, and they are more the result of errors in data collection than a characteristic of a data set.
Outlier detection and potential removal from a data set can be described as a process of the selection of k out of n samples that are considerably dissimilar, exceptional, or inconsistent with respect to the remaining data (k n). The problem of defining outliers is nontrivial, especially in multidimensional samples. The main types of outlier detection schemes are
n). The problem of defining outliers is nontrivial, especially in multidimensional samples. The main types of outlier detection schemes are
- graphical or visualization techniques,
- statistical-based techniques,
- distance-based techniques, and
- model-based techniques.
Examples of visualization methods include Boxplot (1-D), Scatter plot (2-D), and Spin plot (3-D), and they will be explained in the following chapters. Data visualization methods that are useful in outlier detection for one to three dimensions are weaker in multidimensional data because of a lack of adequate visualization methodologies for n-dimensional spaces. An illustrative example of a visualization of 2-D samples and visual detection of outliers is given in Figures
2.6
and
2.7
. The main limitations of the approach are its time-consuming process and the subjective nature of outlier detection.
Figure 2.6.
Outliers for univariate data based on mean value and standard deviation.
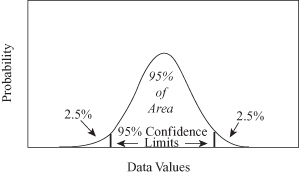
Figure 2.7.
Two-dimensional data set with one outlying sample.

Statistically based outlier detection methods can be divided between
univariate methods
, proposed in earlier works in this field, and
multivariate methods
, which usually form most of the current body of research. Statistical methods either assume a known underlying distribution of the observations or, at least, they are based on statistical estimates of unknown distribution parameters. These methods flag as outliers those observations that deviate from the model assumptions. The approach is often unsuitable for high-dimensional data sets and for arbitrary data sets without prior knowledge of the underlying data distribution.
Most of the earliest univariate methods for outlier detection rely on the assumption of an underlying known distribution of the data, which is assumed to be identically and independently distributed. Moreover, many discordance tests for detecting univariate outliers further assume that the distribution parameters and the type of expected outliers are also known. Although traditionally the normal distribution has been used as the target distribution, this definition can be easily extended to any unimodal symmetric distribution with positive density function. Traditionally, the sample mean and the sample variance give good estimation for data location and data shape if it is not contaminated by outliers. When the database is contaminated, those parameters may deviate and significantly affect the outlier-detection performance. Needless to say, in real-world data-mining applications, these assumptions are often violated.
The simplest approach to outlier detection for 1-D samples is based on traditional unimodal statistics. Assuming that the distribution of values is given, it is necessary to find basic statistical parameters such as mean value and variance. Based on these values and the expected (or predicted) number of outliers, it is possible to establish the threshold value as a function of variance. All samples out of the threshold value are candidates for outliers as presented in Figure
2.6
. The main problem with this simple methodology is an a priori assumption about data distribution. In most real-world examples, the data distribution may not be known.
For example, if the given data set represents the feature age with 20 different values:
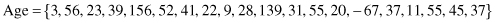
then, the corresponding statistical parameters are