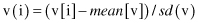Data Mining (8 page)

These rules of the “curse of dimensionality” most often have serious consequences when dealing with a finite number of samples in a high-dimensional space. From properties (1) and (2) we see the difficulty of making local estimates for high-dimensional samples; we need more and more samples to establish the required data density for performing planned mining activities. Properties (3) and (4) indicate the difficulty of predicting a response at a given point, since any new point will on average be closer to an edge than to the training examples in the central part.

One interesting experiment, performed recently by a group of students, shows the importance of understanding curse-of-dimensionality concepts for data-mining tasks. They generated randomly 500 points for different n-dimensional spaces. The number of dimensions was between 2 and 50. Then, they measured in each space all distances between any pair of points and calculated the parameter P:

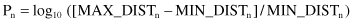
where n is the number of dimensions, and MAX-DIST and MIN-DIST are maximum and minimum distances in the given space, respectively. The results are presented in Figure
2.4
. What is interesting from the graph is that as the number of dimensions increases, the parameter P
_n
approaches the value of 0. That means maximum and minimum distances are becoming very close in these spaces; in other words, there are no differences in distances between any two points in these large-dimensional spaces. It is an experimental confirmation that traditional definitions of density and distance between points, which are critical for many data-mining tasks, change their meaning. When dimensionality of a data set increases, data become increasingly sparse, with mostly outliers in the space that they occupy. Therefore, we have to revisit and reevaluate traditional concepts from statistics: distance, similarity, data distribution, mean, standard deviation, and so on.

Figure 2.4.
With large number of dimensions, the concept of a distance changes the meaning.

2.2 CHARACTERISTICS OF RAW DATA

All raw data sets initially prepared for data mining are often large; many are related to human beings and have the potential for being messy. A priori, one should expect to find missing values, distortions, misrecording, inadequate sampling, and so on in these initial data sets. Raw data that do not appear to show any of these problems should immediately arouse suspicion. The only real reason for the high quality of data could be that the presented data have been cleaned up and preprocessed before the analyst sees them, as in data of a correctly designed and prepared data warehouse.

Let us see what the sources and implications of messy data are. First, data may be
missing
for a huge variety of reasons. Sometimes there are mistakes in measurements or recordings, but in many cases, the value is unavailable. To cope with this in a data-mining process, one must be able to model with the data that are presented, even with their values missing. We will see later that some data-mining techniques are more or less sensitive to missing values. If the method is robust enough, then the missing values are not a problem. Otherwise, it is necessary to solve the problem of missing values before the application of a selected data-mining technique. The second cause of messy data is
misrecording of data
, and that is typical in large volumes of data. We have to have mechanisms to discover some of these “unusual” values, and in some cases, even to work with them to eliminate their influence on the final results. Further, data may
not
be
from the population
they are supposed to be from. Outliers are typical examples here, and they require careful analysis before the analyst can decide whether they should be dropped from the data-mining process as anomalous or included as unusual examples from the population under study.

It is very important to examine the data thoroughly before undertaking any further steps in formal analysis. Traditionally, data-mining analysts had to familiarize themselves with their data before beginning to model them or use them with some data-mining algorithms. However, with the large size of modern data sets, this is less feasible or even entirely impossible in many cases. Here we must rely on computer programs to check the data for us.

Distorted data, incorrect choice of steps in methodology, misapplication of data-mining tools, too idealized a model, a model that goes beyond the various sources of uncertainty and ambiguity in the data—all these represent possibilities for taking the wrong direction in a data-mining process. Therefore, data mining is not just a matter of simply applying a directory of tools to a given problem, but rather a process of critical assessments, exploration, testing, and evaluation. The data should be well-defined, consistent, and nonvolatile in nature. The quantity of data should be large enough to support data analysis, querying, reporting, and comparisons of historical data over a long period of time.

Many experts in data mining will agree that one of the most critical steps in a data-mining process is the preparation and transformation of the initial data set. This task often receives little attention in the research literature, mostly because it is considered too application-specific. But, in most data-mining applications, some parts of a data-preparation process or, sometimes, even the entire process can be described independently of an application and a data-mining method. For some companies with extremely large and often distributed data sets, most of the data-preparation tasks can be performed during the design of the data warehouse, but many specialized transformations may be initialized only when a data-mining analysis is requested.

Raw data are not always (in our opinion very seldom) the best data set for data mining. Many transformations may be needed to produce features more useful for selected data-mining methods such as prediction or classification. Counting in different ways, using different sampling sizes, taking important ratios, varying data-window sizes for time-dependent data, and including changes in moving averages (MA) may all contribute to better data-mining results. Do not expect that the machine will find the best set of transformations without human assistance, and do not expect that transformations used in one data-mining application are the best for another.

The preparation of data is sometimes dismissed as a minor topic in the data-mining literature and used just formally as a phase in a data-mining process. In the real world of data-mining applications, the situation is reversed. More effort is expended preparing data than applying data-mining methods. There are two central tasks for the preparation of data:

2.3 TRANSFORMATION OF RAW DATA

We will review a few general types of transformations of data that are not problem-dependent and that may improve data-mining results. Selection of techniques and use in particular applications depend on types of data, amounts of data, and general characteristics of the data-mining task.

2.3.1 Normalizations

Some data-mining methods, typically those that are based on distance computation between points in an n-dimensional space, may need normalized data for best results. The measured values can be scaled to a specific range, for example, [−1, 1], or [0, 1]. If the values are not normalized, the distance measures will overweight those features that have, on average, larger values. There are many ways of normalizing data. The following are three simple and effective normalization techniques.

Decimal Scaling.

Decimal scaling moves the decimal point but still preserves most of the original digit value. The typical scale maintains the values in a range of −1 to 1. The following equation describes decimal scaling, where v(i) is the value of the feature v for case i and v′(i) is a scaled value

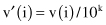
for the smallest k such that
max
(|v′(i)|) < 1.

First, the maximum |v′(i)| is found in the data set, and then the decimal point is moved until the new, scaled, maximum absolute value is less than 1. The divisor is then applied to all other v(i). For example, if the largest value in the set is 455, and the smallest value is −834, then the maximum absolute value of the feature becomes .834, and the divisor for all v(i) is 1000 (k = 3).

Min–Max Normalization.

Suppose that the data for a feature v are in a range between 150 and 250. Then, the previous method of normalization will give all normalized data between .15 and .25, but it will accumulate the values on a small subinterval of the entire range. To obtain better distribution of values on a whole normalized interval, for example, [0,1], we can use the min–max formula

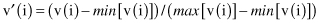
where the minimum and the maximum values for the feature v are computed on a set automatically, or they are estimated by an expert in a given domain. Similar transformation may be used for the normalized interval [−1, 1]. The automatic computation of min and max values requires one additional search through the entire data set, but computationally, the procedure is very simple. On the other hand, expert estimations of min and max values may cause unintentional accumulation of normalized values.

Standard Deviation Normalization.

Normalization by standard deviation often works well with distance measures but transforms the data into a form unrecognizable from the original data. For a feature v, the mean value
mean
(v) and the standard deviation
sd
(v) are computed for the entire data set. Then, for a case i, the feature value is transformed using the equation