My Time in Space (15 page)

Then, in ‘Les Heures Lentes’, a second-hand bookshop that approaches the ideal of such, run by a fragile, melancholy young lady and a massive black-and-white cat usually profoundly asleep in its window, which looks onto a shady little square crowded with café tables, I came across the indefatigably lugubrious rhetoric of Cioran. Opening his
La
Tentation
d’exister,
I found this:

How did that accord with my observations? I was enjoying the baroque theatricality of the side-chapels in Saint-Sauveur for its own sake, the gleams of gold in morbid gloom, the low secretive doors leading away into casuistical labyrinths, the unctuous swell of every form, the swaggering paunch of counter-Reformation Catholicism. But the phrase ‘au siècle des siècles’, ‘ad seculae
seculorum
’, recurring in the Masses we heard or overheard, moved me deeply. If it is the words of the cult, the constant and
continuous
repetition of its formulae over many generations and through an ‘age of ages’, that maintain the cathedral in existence, then without them the building, however well-preserved, is a ruin. And the question preoccupied me: What are cathedrals for, to us who do not sit by the smoky fire of religion?

If the cathedrals are to me primarily storehouses of space, height, darkness and light, and, externally, stone and sky and the sun’s heat, then they are the exact opposite of what they are to the faithful: portals of a transcendent non-material world. What then distinguishes them from secular architecture or even from abstract sculptures? Letting them revert to (mere) stone, to stone for which one cares only aesthetically, would be a catastrophic waste of a millennial resource. But I can hardly call upon the persistence of sempiternal error to support my fleeting truth. Very
approximately
, and as a first guess: for me the cathedral consecrates the here-and-now, the instant, whereas for the believer it conserves
echoes of eternity. It would be easy to stray into spiritual mode and claim the consecrated here-and-now as being precisely an echo of eternity. But while I think that the universe may well be eternal I do not believe in Eternity, either in the form of the Life to Come, the Happy or Unhappy Ever-After, or as the ground, the metaphysical foundation stone, of temporal reality. So what does consecration mean? What do the cathedrals do, beyond the aesthetic, and the always more or less illusory and exploitative rooting, miring, of community in a century of centuries? An urgent question, connected with that of reappropriation (
expropriation
perhaps) of religious language.

Mozart’s
Requiem
in the cathedral; an intent audience, every note crystalline. The vaults of the roof, with many additional vaultings of shadow, contrasting beautifully with the brightly lit stonework of the choir and its seven pointed windows. Looking up at the roof it seems suddenly I am looking up into my own skull, and it has vast room for unknown faculties, it is a mountain seen from within. The visible skeleton of Gothic makes it a
corporeal
style, an extension of ribcage, cranium, the acts of standing, balance, even walking (I think of the lines of columns, and the afternoon light processing from one to the next as the great doors are slowly opened behind us at the end of the concert). Gothic speaks to the skeleton in one’s flesh, the lasting parts: spine,
long-bones
of arms and legs. The person potentially most conscious of this, most uplifted or crushed by it, must be the postulant
prostrated
at the intersection of nave and transept. Cathedrals
intermediate
between body and cosmos, magnifying the former and condensing the latter; they are interpreters between the two, or transformers, adapting the powers of each to the other. Or,
echo-chambers
giving our sense of self back to us from the walls of the
world. When the organist attacks a mighty Passacaglia and Fugue as if intent on testing the building to destruction, sending inertial masses of air crashing from one end to the other of the biggest pipes, flinging treble notes around the vault like cataracts of
shooting
stars, even then the masonry holds, contains and returns to us praise and prayer, confirms our centrality in the structure of being.

For we are only talking to ourselves in such exchanges – even if to the deepest and most rarely addressed levels of ourselves – and we still have to face that which we cannot address and does not address us. Those cathedral-bottled oceanic surges bring me back again to a bleak, disconfirming, edge we lived near once, where, if one shouted, there was no echo because the space beyond was empty. Folklore of the Aran cliffs and those that have fallen from them mentions ‘the step that isn’t there’; if a step is a contract with the earth, this is the one the earth does not honour. Nevertheless one has to enter into such contracts at every moment, to continue in life. The clifftop is a natural emblem for extremal situations, actual or conceptual. One night in Aix I had some thoughts which at the time seemed to represent the
uttermost
reach of the human mind. I doubt I can recapture – not them, but the conviction of their reality and value. Not unusually for dream-thought, they concerned the inexpressible: what it is and why it is so. I risk banality in extracting them from the matrix of drowsy reminiscence in which I found them. I was back on the cliffs, listening to the seethe and crash of waves, hiss of rain, shriek of seabirds; or, trying not to listen, since listening implies selective attention and I wanted to be aware of the whole soundscape at once – barely possible in such a case, with such a spread of
frequencies
, hardly short of white noise, the summation of all
frequencies
. White noise is the absolute nadir of defeated expression,
expression defeating itself by accumulated self-interruption and auto-interference; hence the inevitable collapse of the attempt to express everything simultaneously, sound every note, play every tune. So the inexpressible is the All; it is not to be conflated with the Void, inexpressible only because there is nothing to be expressed. If the All is the Abyss, it is not Tohu-bohu or the
quantum
vacuum, formless source of all things, but the totality of
possible
forms. Expression entails selection and suppression, the gestalt and its background of absence. Hence the inexpressibility of the inexpressible. Nothing, no single thing, is inexpressible, but ‘raids on the inarticulate’ cannot bring home even a fraction of the totality of the expressible. And the reason for that is not just
quantitative
, as to what is to be expressed, the infinite overflow of
subject
-matter, but structural, as to expression itself. My metaphysics is sleepy, but in its sleep it clings to one of my few convictions. For a writer, on this interpretation, the cliff hangs over what
cannot
be written. Maybe one can gesture towards it with such strangely expressive words as ‘inexpressible’ and the mysteriously descriptive ‘undescribable’; or one can enact it, as I have tried to do, exhausting myself in pursuit of
inexhaustible possibilities, dancing on the edge. Perhaps that space beyond is visited by the mystic. In fact, it is tempting, the great circling fulmar-flight into the ineffable; but a profound distrust holds me back from it, a conviction that my task is here, guided by some such
compass-rose
as the little roundels of buckshorn plantain I find appressed to the ground on the very brink of Aran’s cliffs.

There are, however, simpler and more basic interpretations, to restore a cutting edge to this soliloquy. The long cliff-sequence, the hundred pages of ‘South’ in
Stones
of
Aran,
can be read as a meditation on death. A thought of suicide, suppressed from that
book, could find its place in the section called ‘Perdition’s Edge’. Occasionally when we were in wintry mood M and I would visit it – climbing the barren hill to the prehistoric cliff-fort of Dún Aonghasa, skirting its gloomy walls and following the windy clifftop a hundred yards farther west to a projecting angle called Carraig an Smáil, which an island author used to render as the Rock of Perdition. We knew what waves would be thundering against the wall of rock below on such a day, having watched them often and intently on lower shores; they bulge, burst, spout, gape and founder so individually one could give each a proper name – Stag-head, Sloppy Jim, The Walrus, Seven Hills,
Hullabaloo
– wave after wave, hour after hour, day after day. But from this height all that flux of identity was abstracted by distance into a slow regular hammering. We would lie face down on the almost bare stone of the clifftop and work our way forward until our heads stuck out over the appalling drop like gargoyles from a cathedral’s eaves. But this was the anti-cathedral, the smithy of natural law; all things are on the anvil, they shall be thus and thus. Each blow shook the land and was transmitted to our frail soft bodies. Our minds too were shaken. After a time, immeasurable although perhaps brief, we would withdraw, reshaped, annealed, and take ourselves dizzily homewards, our personalities
temporarily
in a vanishing perspective.

If such a cliff can be a renewal, it is because it is also a means, invitation and temptation, to end one’s life. Just four and a half seconds, I calculate, would separate – by what sublime panic? – the last step on earth from obliteration of the self. Believing that the right to one’s own death is essential to one’s personhood, however its exercise is subject to individual and communal
obligations
, I should find it possible to discuss ways and means in a
usual tone. To throw myself off the cliffs that I have written up at such length would be fitting, to the point of melodrama. But nobody thereafter would be able to read me unconstrained by a fateful commentary; I would have permanently conditioned the reception of my work, at least until the reading world had
forgotten
either or both of it and me. Then there are the
practicalities
. It is a strenuous climb to this point, or would be for one suffering terminal illness, terminal sorrow; this is no death for the dying. Also, the kindly folk of Gort na gCapall would inherit the horrible task of finding and retrieving the ruins of my body. And, even if I got so far, exhibited such life-powers, could I nerve myself to the act? I have imagined it and dreamed it too often. The rollers curve in and are reflected back from the cliff with the regularity of balance-wheels, escapements, ratchets; I am falling into the teeth of the world’s clockwork…. At what should have been the last, or nearly the last, moment, flesh and bone would wrench themselves away from the edge, and I would creep home to shameful continuance of life.

What strange relativity is this, that one sees another’s last years as decline, whereas to the person who treads it with such effort the way is uphill, the ground ever steeper, the breath ever shorter. Finally there is no more ground, no more breath. If one could then come down from that painfully attained summit like a
triumphant
mountaineer, to admiring toasts and a well-paid lecture tour! But one cannot share this lonely heroism, though it is
written
into the genes of all mortals, or even savour it in solitude, for clouds of forgetfulness and bewilderment close in. There is not even a view to reward the climber, neither a panorama of the
biographical
archipelago nor an upwards vision of eternity;
consciousness
constricts itself into bone-ache.

No, of course, with luck, with love, with forethought, it may not, need not, come to this. Part of my forethought has been this deathly and unrealistic fantasy of the cliff. But if it is not to be the cliff, discussion of it is not matter for this book, and so I leave it. May it go easily, the untwisting of the threads of my life, and of that other life braided into mine! I am very much afraid of it.

Pascal, before I opened biographies, was chiefly known to me for three pronouncements: his wager on salvation, his confession of cosmic agoraphobia, and his theorem. The first – ‘If God does not exist, one will lose nothing by believing in him, while if he does exist, one will lose everything by not believing’ – is unworthy of both God and human. The second, a mere whisper – ‘Le silence de ces espaces infinis m’effraie’ – still rattles the windows of
civilization
, and I shall follow its echoes in another essay. The third is this:

Ever since I came across it, in my first year at Cambridge, it has been my paradigm of mathematical beauty. When I go now to refresh my memory of its proof in a little textbook of projective
geometry that has followed me around since then, I find a hole from which the relevant diagram has been cut out, reminding me that I used it (in those pre-photocopier days) to illustrate an
article
I wrote for a college magazine. I suspect that my jejune
reflections
on abstract art, maths and Eastern calligraphy would not have been accepted for publication had I not also been the editor; but one point from the essay comes in handy here. The geometrical air of some modernist art (I was thinking of my hero Mondrian, and Gabo and Hepworth among others) might lead one to
suppose
that the beauty of such works is in some way dependent on the beauty of mathematics; however, descriptions of them as
geometrical
configurations would not be of much interest to a
mathematician
. Conversely, the diagram exemplifying a theorem may or may not be beautiful, but the beauty of the theorem itself derives from invisible considerations such as the richness of
connections
it reveals among different mathematical ideas, its ‘
seriousness
’. I borrowed this term from G.H. Hardy’s
A
Mathematician’s
Apology,
that high-minded extension of the Bloomsbury ethos to mathematics. Hardy further analyzes a theorem’s ‘seriousness’ as dependent upon its ‘generality’ or relevance to a wide but well-discriminated body of ideas, and its ‘depth’, by which he seems to mean something like its explanatory power in the hierarchy of concepts. Nowadays I can recognize that my mathematical
preferences
are influenced by less purist factors as well: in this instance by the association of the theorem with Pascal’s fast-burning lifestory, and indeed with the sound of his name, which promises both Gallic grace and passionate intellectuality.

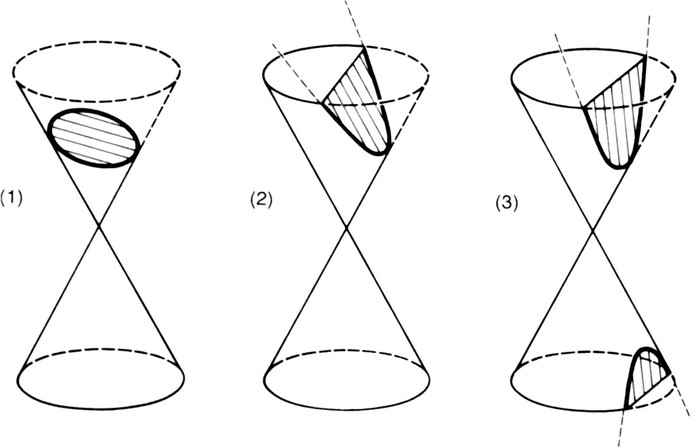
Figs. 1–3. Cross sections of the cone: (1) the ellipse; (2) the parabola; (3) the hyperbola. Only the central portion of the cone is shown; a complete cone has two ‘branches’, each of which extends to infinity. In (3) the cross-section cuts both branches, and so the hyperbola also has two branches.

In the language of geometry a hexagon need not be the sort of honeycomb-cell shape we call by that name in daily life; any six points joined into a circuit by six lines constitute a hexagon, even
if the lines cross one another. (I will say simply ‘line’, instead of specifying each time a straight line.) A conic (or conic section) is any of the curves obtained by taking a cross-section of a cone (Figs. 1–3). The circle is the simplest of them, and the others are familiar presences to those who read by night: the ellipse of light cast on the ceiling from the circular aperture in the top of a tilted lampshade, and the lovely and evocative shape it projects onto a nearby wall, elegantly rounded below and fading away upwards with the grace of an angel’s wing until clipped by the ceiling – a parabola if the two limbs of the illuminated area would eventually become parallel, part of a hyperbola if they would diverge forever. Pascal’s theorem, then, is a powerful generalization, covering any of the endless variety of hexagons that can be inscribed in a conic
of any type or size. A watertight proof of it, starting from the basic definitions and axioms of lines and their intersections, is lengthy and involved. But one can almost
see
that it must be true, by
looking
at a few examples, starting with a very simple case: Take six points evenly distributed around a circle, A, B, C, D, E and F, and join them up in this order: ADBFCE and so back to A (Fig. 4). Calling AD the first side, the side opposite to it is the fourth, FC, and they intersect in X. The second side is DB and it intersects the fifth, CE, in Y. Finally the third side, BF, intersects the sixth, EA, in Z. Then, the diagram being perfectly symmetrical, it is obvious that X, Y and Z lie on a straight line.

Now join up the same six points in another hexagon thus: ADEFCB and back to A (Fig. 5). This time, to find the
intersection
of opposite sides DE and CB, for instance, we have to extend them. But, once again, from symmetry, the three crucial points (as I will call them) lie on a line. And a few experiments with less symmetrical hexagons will convince one that the theorem is
certainly
true for circles (Fig. 6).

Next, imagine any such diagram of a hexagon in a circle being constructed out of strings stretched across that aperture in the top of a lampshade. The doctored lampshade will throw a shadow
diagram
onto a wall or ceiling, showing a hexagon of some sort inscribed in a conic of some sort – and, since the shadows of straight lines are themselves straight, the crucial points in that
diagram
will lie in a line (Fig. 7). Surely enough examples have been exhibited to convince reason that Pascal’s theorem is a general truth? Proving it – proving that there are no exceptions – is of course another story. (Pascal did so at the age of sixteen.) A
complication
arises if two opposite sides are parallel, but they can be considered to meet at infinity; if all three crucial points are
infinitely 
far away, one can take them to lie on a conceptual ‘line at infinity’ – or one can ignore such anomalous cases, infinity being one of the more easily ignored aspects of the world.

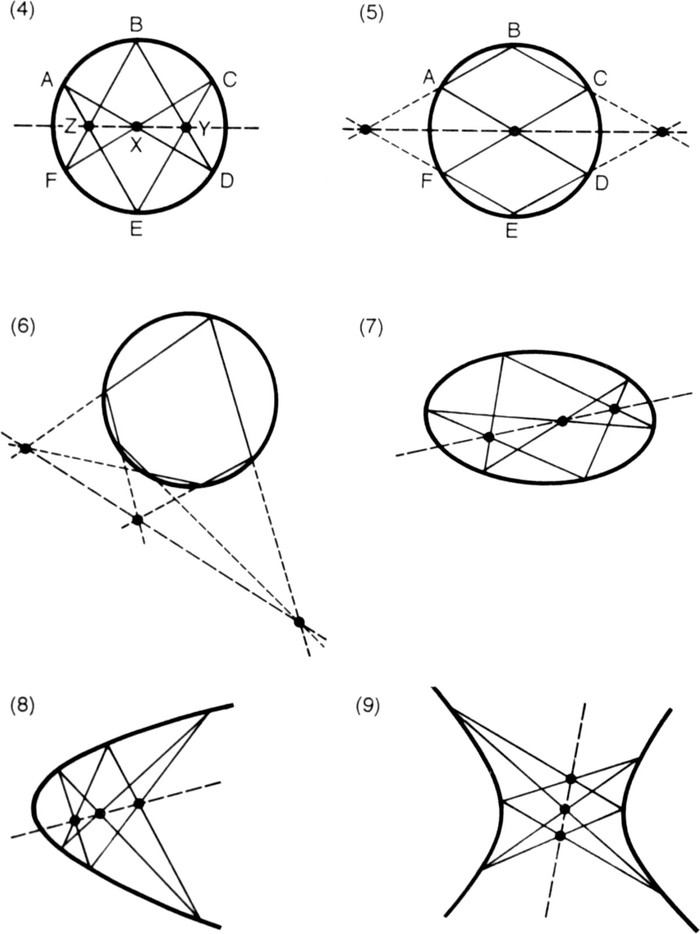
Figs. 4–9. Instances of Pascal’s Theorem.

I have deliberately surrounded this theorem with images of lamps projecting pools of light and of shapes projecting shadows. Pascal’s is one of many theorems that survive projection; the conic may have its shape altered (a circle may become a parabola, for instance, as in Fig. 8), the sides of the hexagon may become longer or shorter and its angles larger or smaller, but the crucial points will still lie on a line. But most of the theorems in Euclid do not remain true under projection. The theorem that the two tangents from a point to a circle are equal, for example; project a diagram of it obliquely, and the circle will become an ellipse and the two tangents unequal. In general, distances and angles are changed by projection, but Pascal’s theorem makes no mention of them; it belongs to a stratum of geometry more basic (deeper, in Hardy’s sense) than the geometry of distances and angles.

Frustratingly, it is not known how Pascal proved his theorem. The result was announced without proof in 1640 in his first
published
work, a leaflet which is hardly more than an advertisement for a proposed treatise, circulated among the scientists of the day including Huygens, who forwarded it immediately to Descartes. After some basic definitions Pascal states two lemmas, of which the first is his theorem, for the case of a circle. (It is not in the trenchant and symmetrical form he later gave the result, and the hexagon is not explicitly mentioned, but the result is equivalent to what we now call Pascal’s Theorem.) From these he proposes to show that the same is true of any conic section, and thence deduce all the elements of conies, including the subject’s basic theorem, due to his elder contemporary Desargues, to whom he almost over-modestly acknowledges his debt: ‘I owe the little I have discovered on this topic to his writings, and … I have tried to imitate his method, so far as was possible for me.’ There was a
certain rivalry between Descartes’ algebraic approach to geometry and Desargues’ more intuitive and visual methods, and perhaps this made Descartes read too hastily, for he mistakenly jumped to the conclusion that the youngster had not done more than imitate Desargues; later on he came to appreciate Pascal’s genius, and was especially interested in his experiments on vacuums or
‘la
Vide’.

From the correspondence of Pascal’s mathematical mentor Père Mersenne later in 1640 we learn that Pascal deduced four hundred corollaries from his theorem, covering the field of
Apollonius’s
treatise, the ancient classic on conies, and that the work was to be published in the following year. Desargues himself
followed
its progress, and referred in his own writings to ‘this great proposition called
la
Pascale
’. However, although Pascal published work on other branches of mathematics (and designed and built the first calculating machine), the promised
Traité
des
coniques
never appeared. When Fermat, with whom he had corresponded on and effectively co-founded the theory of probability, wrote to him in 1660 suggesting a meeting, he replied with expressions of esteem for ‘Europe’s greatest geometer’ (‘geometer’ here meaning ‘mathematician’), but sickness and his increasingly demanding religiosity reduced him to the saddening admission, ‘I would not take two steps for geometry … I am engaged in studies so far from that turn of mind I scarcely remember what it is about.’ We are all the losers by Pascal’s miscalculated wager on God.

After his early death Pascal’s manuscripts on conies were sent by his family to Leibniz, a great admirer, whose own achievement in founding what we now call analysis or calculus owed much to Pascal. Leibniz sorted them out into five treatises, had a copy made of the first, and returned them with a letter summarizing their contents, concluding by stating that ‘This work is in fit state
to be printed, and there is no question that it merits it.’
Unforgivably
, the family did not act on this advice. The manuscripts were seemingly deposited with Pascal’s other papers at Saint-
Germain
-des-Prés, and are now lost. One feels like demanding that all the archives in which they could possibly be lying suspend all other business while they turn themselves inside-out like sacks to find them. As it is we have Leibniz’s copy of the first treatise and his letter, from which it appears that the second treatise contained the proof of the theorem Pascal himself called the ‘Hexagramme mystique’, the consequences of which were elaborated in the
subsequent
treatises. The penetrating luminosity of the first treatise gives one a heightened sense of what is lost.

In the leaflet of 1640 the theorem is first stated for a circle, and then extended to the general conic. It seems clear that Pascal’s method of doing this was to be by projection. In the first treatise he gives his definition of a cone, which amounts to this: if a line is drawn through a point on a circle and another fixed point not in the plane of the circle, then as the first point is allowed to move around the circle, the line sweeps out the surface of a cone (Fig. 10). And he deduces the properties of the various conic sections from those of the circle, by imagining that the eye is placed at the vertex of the cone, so that the conic is the image of the circle; i.e. points of the conic coincide visually with those of the circle. (This eye is highly idealized; it sees in all directions.) Leibniz, it appears from his private notes, was surprised and seduced by this ‘optical method of cast shadows’ and wondered if it could not ‘transcend the cone and rise to higher considerations’, that is to a general projective geometry not limited to lines and conics, which of course has come to pass.