The Information (32 page)

The theorem was an extension of Nyquist’s formula, and it could be expressed in words: the most information that can be transmitted in any given time is proportional to the available frequency range (he did not yet use the term
bandwidth
). Hartley was bringing into the open a set of ideas and assumptions that were becoming part of the unconscious culture of electrical engineering, and the culture of Bell Labs especially. First was the idea of information itself. He needed to pin a butterfly to the board. “As commonly used,” he said, “information is a very elastic term.”
♦
It is the stuff of communication—which, in turn, can be direct speech, writing, or anything else. Communication takes place by means of symbols—Hartley cited for example “words” and “dots and dashes.” The symbols, by common agreement, convey “meaning.” So far, this was one slippery concept after another. If the goal was to “eliminate the psychological factors involved” and to establish a measure “in terms of purely physical quantities,” Hartley needed something definite and countable. He began by counting symbols—never mind what they meant. Any transmission contained a countable number of symbols. Each symbol represented a choice; each was selected from a certain set of possible symbols—an alphabet, for example—and the number of
possibilities, too, was countable. The number of possible words is not so easy to count, but even in ordinary language, each word represents a selection from a set of possibilities:
For example, in the sentence, “Apples are red,” the first word eliminated other kinds of fruit and all other objects in general. The second directs attention to some property or condition of apples, and the third eliminates other possible colors.…
The number of symbols available at any one selection obviously varies widely with the type of symbols used, with the particular communicators and with the degree of previous understanding existing between them.
♦
Hartley had to admit that some symbols might convey more information, as the word was
commonly
understood, than others. “For example, the single word ‘yes’ or ‘no,’ when coming at the end of a protracted discussion, may have an extraordinarily great significance.” His listeners could think of their own examples. But the point was to subtract human knowledge from the equation. Telegraphs and telephones are, after all, stupid.
It seemed intuitively clear that the amount of information should be proportional to the number of symbols: twice as many symbols, twice as much information. But a dot or dash—a symbol in a set with just two members—carries less information than a letter of the alphabet and much less information than a word chosen from a thousand-word dictionary. The more possible symbols, the more information each selection carries. How much more? The equation, as Hartley wrote it, was this:
H
=
n
log
s
where
H
is the amount of information,
n
is the number of symbols transmitted, and
s
is the size of the alphabet. In a dot-dash system,
s
is just 2. A single Chinese character carries so much more weight than a Morse dot or dash; it is so much more valuable. In a system with a symbol for every word in a thousand-word dictionary,
s
would be 1,000.
The amount of information is not proportional to the alphabet size, however. That relationship is logarithmic: to double the amount of information, it is necessary to quadruple the alphabet size. Hartley illustrated this in terms of a printing telegraph—one of the hodgepodge of devices, from obsolete to newfangled, being hooked up to electrical circuits. Such telegraphs used keypads arranged according to a system devised in France by Émile Baudot. The human operators used keypads, that is—the device translated these key presses, as usual, into the opening and closing of telegraph contacts. The Baudot code used five units to transmit each character, so the number of possible characters was 2
5
or 32. In terms of information content, each such character was five times as valuable—not thirty-two times—as its basic binary units.
Telephones, meanwhile, were sending their human voices across the network in happy, curvaceous analog waves. Where were the symbols in those? How could they be counted?
Hartley followed Nyquist in arguing that the continuous curve should be thought of as the limit approached by a succession of discrete steps, and that the steps could be recovered, in effect, by sampling the waveform at intervals. That way telephony could be made subject to the same mathematical treatment as telegraphy. By a crude but convincing analysis, he showed that in both cases the total amount of information would depend on two factors: the time available for transmission and the bandwidth of the channel. Phonograph records and motion pictures could be analyzed the same way.
These odd papers by Nyquist and Hartley attracted little immediate attention. They were hardly suitable for any prestigious journal of mathematics or physics, but Bell Labs had its own,
The Bell System Technical Journal
, and Claude Shannon read them there. He absorbed the mathematical insights, sketchy though they were—first awkward steps toward a shadowy goal. He noted also the difficulties both men had in defining their terms. “By the speed of transmission of intelligence is meant the number of characters, representing different letters, figures, etc., which
can be transmitted in a given length of time.”
♦
Characters, letters, figures: hard to count. There were concepts, too, for which terms had yet to be invented: “the capacity of a system to transmit a particular sequence of symbols …”
♦
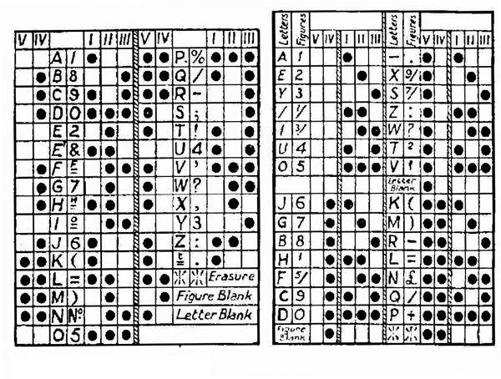
THE BAUDOT CODE
Shannon felt the promise of unification. The communications engineers were talking not just about wires but also the air, the “ether,” and even punched tape. They were contemplating not just words but also sounds and images. They were representing the whole world as symbols, in electricity.
♦
In an evaluation forty years later the geneticist James F. Crow wrote: “It seems to have been written in complete isolation from the population genetics community.…[Shannon] discovered principles that were rediscovered later.… My regret is that [it] did not become widely known in 1940. It would have changed the history of the subject substantially, I think.”
♦
In standard English, as Russell noted, it is one hundred and eleven thousand seven hundred and seventy-seven.
(All I’m After Is Just a Mundane Brain)
Perhaps coming up with a theory of information and its processing is a bit like building a transcontinental railway. You can start in the east, trying to understand how agents can process anything, and head west. Or you can start in the west, with trying to understand what information is, and then head east. One hopes that these tracks will meet.
—Jon Barwise (1986)
♦
AT THE HEIGHT OF THE WAR
, in early 1943, two like-minded thinkers, Claude Shannon and Alan Turing, met daily at teatime in the Bell Labs cafeteria and said nothing to each other about their work, because it was secret.
♦
Both men had become cryptanalysts. Even Turing’s presence at Bell Labs was a sort of secret. He had come over on the
Queen Elizabeth
, zigzagging to elude U-boats, after a clandestine triumph at Bletchley Park in deciphering Enigma, the code used by the German military for its critical communication (including signals to the U-boats). Shannon was working on the X System, used for encrypting voice conversations between Franklin D. Roosevelt at the Pentagon and Winston Churchill in his War Rooms. It operated by sampling the analog voice signal fifty times a second—“quantizing” or “digitizing” it—and masking it by applying a random key, which happened to bear a strong resemblance to the circuit noise with which the engineers were so familiar. Shannon did not design the system; he was assigned to analyze it theoretically
and—it was hoped—prove it to be unbreakable. He accomplished this. It was clear later that these men, on their respective sides of the Atlantic, had done more than anyone else to turn cryptography from an art into a science, but for now the code makers and code breakers were not talking to each other.
With that subject off the table, Turing showed Shannon a paper he had written seven years earlier, called “On Computable Numbers,” about the powers and limitations of an idealized computing machine. They talked about another topic that turned out to be close to their hearts, the possibility of machines learning to think. Shannon proposed feeding “cultural things,” such as music, to an electronic brain, and they outdid each other in brashness, Turing exclaiming once, “No, I’m not interested in developing a
powerful
brain. All I’m after is just a
mundane
brain, something like the president of the American Telephone & Telegraph Company.”
♦
It bordered on impudence to talk about thinking machines in 1943, when both the transistor and the electronic computer had yet to be born. The vision Shannon and Turing shared had nothing to do with electronics; it was about logic.
Can machines think
? was a question with a relatively brief and slightly odd tradition—odd because machines were so adamantly physical in themselves. Charles Babbage and Ada Lovelace lay near the beginning of this tradition, though they were all but forgotten, and now the trail led to Alan Turing, who did something really outlandish: thought up a machine with ideal powers in the mental realm and showed what it could
not
do. His machine never existed (except that now it exists everywhere). It was only a thought experiment.
Running alongside the issue of what a machine could do was a parallel issue: what tasks were
mechanical
(an old word with new significance). Now that machines could play music, capture images, aim antiaircraft guns, connect telephone calls, control assembly lines, and perform mathematical calculations, the word did not seem quite so pejorative. But only the fearful and superstitious imagined that machines could be creative
or original or spontaneous; those qualities were opposite to
mechanical
, which meant automatic, determined, and routine. This concept now came in handy for philosophers. An example of an intellectual object that could be called mechanical was the algorithm: another new term for something that had always existed (a recipe, a set of instructions, a step-by-step procedure) but now demanded formal recognition. Babbage and Lovelace trafficked in algorithms without naming them. The twentieth century gave algorithms a central role—beginning here.
Turing was a fellow and a recent graduate at King’s College, Cambridge, when he presented his computable-numbers paper to his professor in 1936. The full title finished with a flourish in fancy German: it was “On Computable Numbers, with an Application to the
Entscheidungsproblem
.” The “decision problem” was a challenge that had been posed by David Hilbert at the 1928 International Congress of Mathematicians. As perhaps the most influential mathematician of his time, Hilbert, like Russell and Whitehead, believed fervently in the mission of rooting all mathematics in a solid logical foundation—
“In der Mathematik gibt es kein Ignorabimus,”
he declared. (“In mathematics there is no
we will not know
.”) Of course mathematics had many unsolved problems, some quite famous, such as Fermat’s Last Theorem and the Goldbach conjecture—statements that seemed true but had not been proved. Had not
yet
been proved, most people thought. There was an assumption, even a faith, that any mathematical truth would be provable, someday.
The
Entscheidungsproblem
was to find a rigorous step-by-step procedure by which, given a formal language of deductive reasoning, one could perform a proof automatically. This was Leibniz’s dream revived once again: the expression of all valid reasoning in mechanical rules. Hilbert posed it in the form of a question, but he was an optimist. He thought or hoped that he knew the answer. It was just then, at this watershed moment for mathematics and logic, that Gödel threw his incompleteness theorem into the works. In flavor, at least, Gödel’s result seemed a perfect antidote to Hilbert’s optimism, as it was to Russell’s. But Gödel
actually left the
Entscheidungsproblem
unanswered. Hilbert had distinguished among three questions:
Is mathematics complete?
Is mathematics consistent?
Is mathematics decidable?