The Information (35 page)

Fire control and cryptography aside, Shannon had been pursuing this haze of ideas all through the war. Living alone in a Greenwich Village apartment, he seldom socialized with his colleagues, who mainly worked now in the New Jersey headquarters, while Shannon preferred the old West Street hulk. He did not have to explain himself. His war work got him deferred from military service and the deferment continued after the war ended. Bell Labs was a rigorously male enterprise, but in wartime the computing group, especially, badly needed competent staff and began hiring women, among them Betty Moore, who had grown up on Staten Island. It was like a typing pool for math majors, she thought. After a
year she was promoted to the microwave research group, in the former Nabisco building—the “cracker factory”—across West Street from the main building. The group designed tubes on the second floor and built them on the first floor and every so often Claude wandered over to visit. He and Betty began dating in 1948 and married early in 1949. Just then he was the scientist everyone was talking about.

THE WEST STREET HEADQUARTERS OF BELL LABORATORIES, WITH TRAINS OF THE HIGH LINE RUNNING THROUGH
Few libraries carried
The Bell System Technical Journal
, so researchers heard about “A Mathematical Theory of Communication” the traditional way, by word of mouth, and obtained copies the traditional way, by writing directly to the author for an offprint. Many scientists used preprinted postcards for such requests, and these arrived in growing volume over the next year. Not everyone understood the paper. The mathematics was difficult for many engineers, and mathematicians meanwhile lacked the engineering context. But Warren Weaver, the director of natural sciences for the Rockefeller Foundation uptown, was already telling his president that Shannon had done for communication theory “what Gibbs did for physical chemistry.”
♦
Weaver had headed the government’s applied mathematics research during the war, supervising the fire-control project as well as nascent work in electronic calculating machines. In 1949 he wrote up an appreciative and not too technical essay about Shannon’s theory for
Scientific American
, and late that year the two pieces—Weaver’s essay and Shannon’s monograph—were published together as a book, now titled with a grander first word
The Mathematical Theory of Communication
. To John Robinson Pierce, the Bell Labs engineer who had been watching the simultaneous gestation of the transistor and Shannon’s paper, it was the latter that “came as a bomb, and something of a delayed action bomb.”
♦
Where a layman might have said that the fundamental problem of communication is to make oneself understood—to convey meaning—Shannon set the stage differently:
The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.
♦
“Point” was a carefully chosen word: the origin and destination of a message could be separated in space or in time; information storage, as in a phonograph record, counts as a communication. Meanwhile, the message is not created; it is selected. It is a choice. It might be a card dealt from a deck, or three decimal digits chosen from the thousand possibilities, or a combination of words from a fixed code book. He could hardly overlook meaning altogether, so he dressed it with a scientist’s definition and then showed it the door:
Frequently the messages have
meaning;
that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem.
Nonetheless, as Weaver took pains to explain, this was not a narrow view of communication. On the contrary, it was all-encompassing: “not only written and oral speech, but also music, the pictorial arts, the theatre, the ballet, and in fact all human behavior.” Nonhuman as well: why should machines not have messages to send?
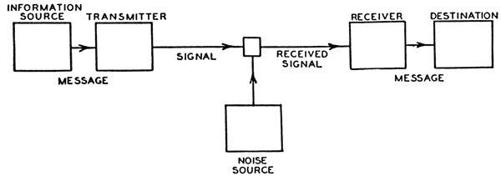
Shannon’s model for communication fit a simple diagram—essentially the same diagram, by no coincidence, as in his secret cryptography paper.
A communication system must contain the following elements:
- The information source is the person or machine generating the message, which may be simply a sequence of characters, as in a telegraph or teletype, or may be expressed mathematically as functions—
f
(
x
,
y
,
t
)—of time and other variables. In a complex example like color television, the components are three functions in a three-dimensional continuum, Shannon noted. - The transmitter “operates on the message in some way”—that is,
encodes
the message—to produce a suitable signal. A telephone converts sound pressure into analog electric current. A telegraph encodes characters in dots, dashes, and spaces. More complex messages may be sampled, compressed, quantized, and interleaved. - The channel: “merely the medium used to transmit the signal.”
- The receiver inverts the operation of the transmitter. It decodes the message, or reconstructs it from the signal.
- The destination “is the person (or thing)” at the other end.
In the case of ordinary speech, these elements are the speaker’s brain, the speaker’s vocal cords, the air, the listener’s ear, and the listener’s brain.
As prominent as the other elements in Shannon’s diagram—because for an engineer it is inescapable—is a box labeled “Noise Source.” This covers everything that corrupts the signal, predictably or unpredictably: unwanted additions, plain errors, random disturbances, static, “atmospherics,” interference, and distortion. An unruly family under any circumstances, and Shannon had two different types of systems to deal with, continuous and discrete. In a discrete system, message and signal take the form of individual detached symbols, such as characters or digits or dots and dashes. Telegraphy notwithstanding, continuous systems of waves and functions were the ones facing electrical engineers every day. Every engineer, when asked to push more information through a channel, knew what to do: boost the power. Over long distances, however, this approach was failing, because amplifying a signal again and again leads to a crippling buildup of noise.
Shannon sidestepped this problem by treating the signal as a string of discrete symbols. Now, instead of boosting the power, a sender can overcome noise by using extra symbols for error correction—just as an African drummer makes himself understood across long distances, not by banging the drums harder, but by expanding the verbosity of his discourse. Shannon considered the discrete case to be more fundamental in a mathematical sense as well. And he was considering another point: that treating messages as discrete had application not just for traditional communication but for a new and rather esoteric subfield, the theory of computing machines.
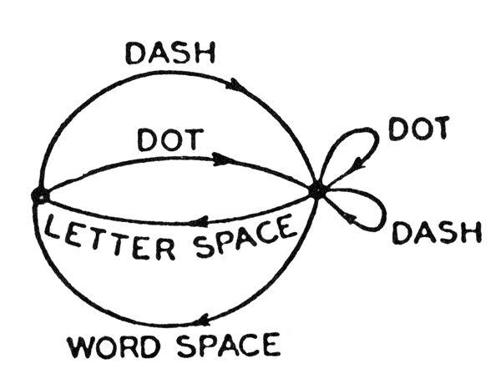
So back he went to the telegraph. Analyzed precisely, the telegraph did not use a language with just two symbols, dot and dash. In the real world telegraphers used dot (one unit of “line closed” and one unit of “line open”), dash (three units, say, of line closed and one unit of line open), and also two distinct spaces: a letter space (typically three units of line open) and a longer space separating words (six units of line open). These four symbols have unequal status and probability. For example, a space can never follow another space, whereas a dot or dash can follow anything. Shannon expressed this in terms of
states
. The system has two states: in one, a space was the previous symbol and only a dot or dash is allowed, and the state then changes; in the other, any symbol is allowed, and the state changes only if a space is transmitted. He illustrated this as a graph:
This was far from a simple, binary system of encoding. Nonetheless Shannon showed how to derive the correct equations for information content and channel capacity. More important, he focused on the effect of the statistical structure of the language of the message. The very existence
of this structure—the greater frequency of
e
than
q
, of
th
than
xp
, and so forth—allows for a saving of time or channel capacity.
This is already done to a limited extent in telegraphy by using the shortest channel sequence, a dot, for the most common English letter E; while the infrequent letters, Q, X, Z are represented by longer sequences of dots and dashes. This idea is carried still further in certain commercial codes where common words and phrases are represented by four- or five-letter code groups with a considerable saving in average time. The standardized greeting and anniversary telegrams now in use extend this to the point of encoding a sentence or two into a relatively short sequence of numbers.
♦
To illuminate the structure of the message Shannon turned to some methodology and language from the physics of stochastic processes, from Brownian motion to stellar dynamics. (He cited a landmark 1943 paper by the astrophysicist Subrahmanyan Chandrasekhar in
Reviews of Modern Physics
.
♦
) A stochastic process is neither deterministic (the next event can be calculated with certainty) nor random (the next event is totally free). It is governed by a set of probabilities. Each event has a probability that depends on the state of the system and perhaps also on its previous history. If for
event
we substitute
symbol
, then a natural written language like English or Chinese is a stochastic process. So is digitized speech; so is a television signal.
Looking more deeply, Shannon examined statistical structure in terms of how much of a message influences the probability of the next symbol. The answer could be none: each symbol has its own probability but does not depend on what came before. This is the first-order case. In the second-order case, the probability of each symbol depends on the symbol immediately before, but not on any others. Then each two-character combination, or digram, has its own probability:
th
greater than
xp
, in English. In the third-order case, one looks at trigrams, and so forth. Beyond that, in ordinary text, it makes sense to look at the level of words rather than individual characters, and many types of statistical
facts come into play. Immediately after the word
yellow
, some words have a higher probability than usual and others virtually zero. After the word
an
, words beginning with consonants become exceedingly rare. If the letter
u
ends a word, the word is probably
you.
If two consecutive letters are the same, they are probably
ll, ee, ss
, or
oo
. And structure can extend over long distances: in a message containing the word
cow
, even after many other characters intervene, the word
cow
is relatively likely to occur again. As is the word
horse
. A message, as Shannon saw, can behave like a dynamical system whose future course is conditioned by its past history.