Three Roads to Quantum Gravity (19 page)
Read Three Roads to Quantum Gravity Online
Authors: Lee Smolin

A few weeks later we went to Syracuse University, which by then was the centre of work stemming from Ashtekar’s and Sen’s discoveries, and Carlo gave the first seminar on the new theory of quantum gravity. On the way to the airport we were rear-ended by a guy in a very flashy car. No one was hurt, and the rear bumper of my old Dodge Dart was barely scratched, but his Maserati was wrecked. Still, we made it. The next day Carlo had a high fever, but he got through the seminar, and at the end there was a long, appreciative silence. Abhay Ashtekar said it was the first time he had seen something that might be the quantum theory of gravity. A few weeks after that I gave the second seminar on the new theory, in London, in front of Chris Isham, on my way to a conference in India.
In India, two ancient cultures met when I introduced the conference organizer to Carlo, who had decided impulsively to jump on a plane and come, though he had no invitation. The distinguished gentleman looked at his long hair and the sandals and clothes he had picked up while wandering alone for two days through the back streets of Bombay, and sputtered, ‘Mr Rovelli, but didn’t you get my letter saying the meeting is closed?’ Carlo smiled and replied, ‘No, but
didn’t you get mine?’ He was given the best room in the hotel, and Air India put him in first class on his flight home to Rome.
didn’t you get mine?’ He was given the best room in the hotel, and Air India put him in first class on his flight home to Rome.
Thus was born what is now called loop quantum gravity. It took several years of work, first with Carlo and then as part of a growing community of friends and colleagues, to unravel the meaning of the solutions to the quantum gravity equations we had found. One straightforward consequence is that quantum geometry is indeed discrete. Everything we had done had been based on the idea of a discrete line of force, as in a magnetic field in a superconductor. Translated into the loop picture of the gravitational field, this turns out to imply that the area of any surface comes in discrete multiples of simple units. The smallest of these units is about the Planck area, which is the square of the Planck length. This means that all surfaces are discrete, made of parts each of which carries a finite amount of area. The same is true of volume.
To arrive at these results we had to find a way to eliminate the infinities that plague all expressions in quantum theories of fields. I had an intuition, stemming from my past conversations with Julian Barbour, and the work I had done with Louis Crane, that the theory should have no infinities. Many physicists have speculated that the infinities come from some mistaken assumption about the structure of space and time on the Planck scale. From the older work it was clear to me that the wrong assumption was the idea that the geometry of spacetime was fixed and non-dynamical. When calculating the measures of geometry, such as area and volume, one had to do it in just the right way to eliminate any possible contamination from non-dynamical, fixed structures. Exactly how to do this was a technical exercise that cannot be explained here. But in the end it did turn out that as long as one asks a physically meaningful question, there will be no infinities.
In my experience it really is true that as a scientist one has only a few good ideas. They are few and far between, and come only after many years of preparation. What is worse, having had a good idea one is condemned to years of hard work developing it. The idea that area and volume would be
discrete had come to me in a flash as I was trying to calculate the volume of some quantum geometry, while I was sitting for an hour in a noisy room in a garage waiting for my car to be fixed. The page of my notebook was filled with many messy integrals, but all of a sudden I saw emerge a formula for counting. I had begun to calculate a quantity on the assumption that the result was a real number, but found instead that, in certain units, all the possible answers would be integers. This meant that areas and volumes cannot take any value, but come in multiples of fixed units. These units correspond to the smallest areas and volumes that can exist. I showed these calculations to Carlo, and a few months later, during a period we spent working together at the University of Trento, in the mountains of north-east Italy, he invented an argument that showed that the basic unit of area could not be taken to zero. This meant there was no way to avoid the conclusion that if our theory were true, space had an ‘atomic’ structure.
discrete had come to me in a flash as I was trying to calculate the volume of some quantum geometry, while I was sitting for an hour in a noisy room in a garage waiting for my car to be fixed. The page of my notebook was filled with many messy integrals, but all of a sudden I saw emerge a formula for counting. I had begun to calculate a quantity on the assumption that the result was a real number, but found instead that, in certain units, all the possible answers would be integers. This meant that areas and volumes cannot take any value, but come in multiples of fixed units. These units correspond to the smallest areas and volumes that can exist. I showed these calculations to Carlo, and a few months later, during a period we spent working together at the University of Trento, in the mountains of north-east Italy, he invented an argument that showed that the basic unit of area could not be taken to zero. This meant there was no way to avoid the conclusion that if our theory were true, space had an ‘atomic’ structure.
I well remember our work in Trento for another reason. In the previous year one of our students, Bernd Bruegmann, had come to my office with a very disturbed look on his face. His thesis problem was to apply the new methods from loop quantum gravity to QCD on a lattice, and see whether the properties of protons and neutrons would emerge. While doing so he did what good scientists should do, but which we had not, which was to check the literature thoroughly. He had found a paper in which methods very similar to ours had already been applied to QCD by two people we had never heard of, Rodolfo Gambini and Anthony Trias, who were working in Montevideo and Barcelona.
Scientists are human, and we all suffer from the need to feel that what we do is important. Pretty much the worst thing that can happen to a scientist is to find that someone has made the same discovery before you. The only thing worse is when someone publishes the same discovery you made, after you’ve published it yourself, and does not give you adequate credit. It was true that we had discovered the method of working with loops in the realm of quantum gravity rather than in QCD, but there was no avoiding the fact that the method we had developed was quite close to the one that Gambini and
Trias had already been using for several years in their work on QCD. Even though they had been publishing in the Physical Review, which is a major journal, we had somehow missed seeing their work.
Trias had already been using for several years in their work on QCD. Even though they had been publishing in the Physical Review, which is a major journal, we had somehow missed seeing their work.
With a heavy heart we did the only thing we could, which was to sit down and write them a very apologetic letter. We heard nothing from them until one afternoon in Trento, when Carlo got a phone call from Barcelona. Our letter had finally reached them. They had tracked us down to Trento, and asked if we would still be there tomorrow. The next morning they arrived, having driven most of the night across France and northern Italy. We spent a wonderful day showing each other our work, which was thankfully complementary. They had applied the method to QCD, while we had applied it to quantum gravity. Anthony Trias did most of the talking, while Rodolfo Gambini sat at the back of the room and at first hardly said anything. But we soon found that Rodolfo was a creative scientist of the first order. Just how creative we learned over the next few months, as he quickly invented a new approach to doing calculations in loop quantum gravity.
Since then Gambini has been one of the leaders in the field of quantum gravity, often working in collaboration with Jorge Pullin at Penn State University and a very good group of young people he trained in Montevideo. They have discovered many more solutions to the equations of quantum gravity, and resolved several important problems that came up along the way.
It also must be said that, despite his quiet nature, Rodolfo Gambini has been more or less single-handedly responsible for reviving physics in both Venezuela and Uruguay after its total destruction by the military dictatorships. Just what this meant was brought home to me the first time I visited Montevideo. It was the middle of winter, and we did physics with Rodolfo and his group in a run-down old convent, without heat or computers, fighting off the cold by drinking a continuous supply of matte (a kind of tea) that was kept hot over a Bunsen burner. Now the science departments at the University of Uruguay are housed in modern buildings and
facilities, built with funds that Rodolfo raised in his spare time, while keeping up a continuous flow of new ideas and calculations.
facilities, built with funds that Rodolfo raised in his spare time, while keeping up a continuous flow of new ideas and calculations.
One of the most beautiful results to have come from loop quantum gravity was the discovery that the loop states could be arranged in very beautiful pictures, which are called spin networks. These had actually been invented thirty years earlier by Roger Penrose. Penrose had also been inspired by the idea that space must be purely relational. Going directly to the heart of the matter, as is his nature, he had skipped the step of trying to derive a picture of relational space from some existing theory, as we had. Instead, having more courage, he had sought the simplest possible relational structure that might be the basis of a quantum theory of geometry. Spin networks were what he came up with. A spin network is simply a graph, such as those shown in
Figures 24
to
27
, whose edges are labelled by integers. These integers come from the values that the angular momentum of a particle are allowed to have in quantum theory, which are equal to an integer times half of Planck’s constant.
Figures 24
to
27
, whose edges are labelled by integers. These integers come from the values that the angular momentum of a particle are allowed to have in quantum theory, which are equal to an integer times half of Planck’s constant.

A spin network, as invented by Roger Penrose, also represents a quantum state of the geometry of space. It consists of a graph, together with integers on the edges. Only a few of the numbers are shown here.
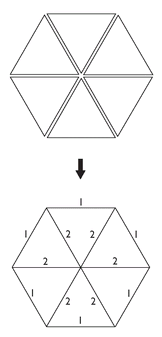
FIGURE 25
A spin network can be made by combining loops.
I had known for a long time that Penrose’s spin networks should come into loop quantum gravity, but I had been afraid of working with them. When Penrose described them in his talks they always seemed so intricate that only he would be able to work with them without making mistakes. To do a calculation Penrose’s way, one has to add up long series of numbers which are each either +1, 0 or -1. If you miss one sign, you’re dead. Still, during a visit to Cambridge in 1994 I met Roger and asked him to tell me how to calculate with his spin networks. We did one calculation together, and I thought I had the hang of it. That was enough to convince me that spin networks would make it possible to calculate aspects of quantum geometry such as the smallest possible volume. I then showed what I had learned to Carlo, and we spent the rest of that summer translating our theory into the language of Penrose’s spin networks.
When we did this we found that each spin network gives a possible quantum state for the geometry of space. The integers
on each edge of a network correspond to units of area carried by that edge. Rather than carrying a certain amount of electric or magnetic flux, the lines of a spin network carry units of area. The nodes of the spin networks also have a simple meaning: they correspond to quantized units of volume. The volume contained in a simple spin network, when measured in Planck units, is basically equal to the number of nodes of the network. It took much work and heartache to clarify this picture. Penrose’s method was invaluable but, as I had expected, it was not easy to work with. Along the way we learned the truth of something I once heard Richard Feynman say, which is that a good scientist is someone who works hard enough to make every possible mistake before coming to the right answer.
on each edge of a network correspond to units of area carried by that edge. Rather than carrying a certain amount of electric or magnetic flux, the lines of a spin network carry units of area. The nodes of the spin networks also have a simple meaning: they correspond to quantized units of volume. The volume contained in a simple spin network, when measured in Planck units, is basically equal to the number of nodes of the network. It took much work and heartache to clarify this picture. Penrose’s method was invaluable but, as I had expected, it was not easy to work with. Along the way we learned the truth of something I once heard Richard Feynman say, which is that a good scientist is someone who works hard enough to make every possible mistake before coming to the right answer.

FIGURE 26
The quantization of space as predicted by loop quantum gravity. The edges of spin networks carry discrete units of area. The area of a surface comes from the intersection of one edge of a spin network with it. The smallest possible area comes from one intersection, and is about 10
-66
of a square centimetre. The nodes of the spin networks carry discrete units of volume. The smallest possible volume comes from one node, and is about 10
-99
of a cubic centimetre.
-66
of a square centimetre. The nodes of the spin networks carry discrete units of volume. The smallest possible volume comes from one node, and is about 10
-99
of a cubic centimetre.
Other books
Burning Blue by Paul Griffin
Lost in the Apocalypse by Mortimer, L.C.
Dancing With Devia by Viveca Benoir
White Chocolate Moments by Lori Wick
A Summer In Europe by Marilyn Brant
Icons by Margaret Stohl
High-Wired by Andrea Frazer
The Dog That Saved Stewart Coolidge by Jim Kraus
Trilby by Diana Palmer