Three Roads to Quantum Gravity (20 page)

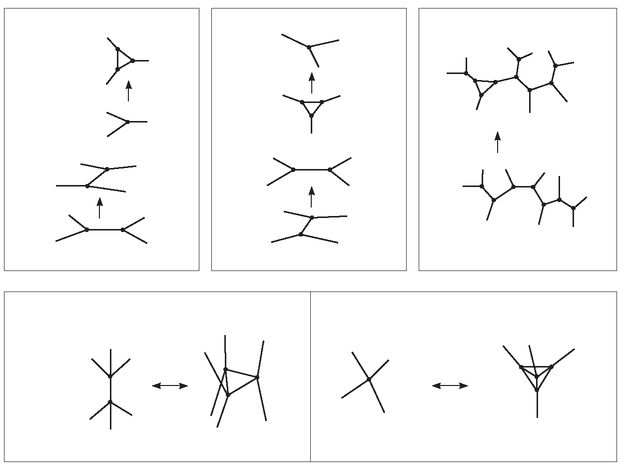
A very large spin network can represent a quantum geometry that looks smooth and continuous when viewed on a scale much larger than the Planck length. We say that the classical geometry of space is woven by making it out of a very large and complex spin network. In the spin network picture, space only seems continuous - it is actually made up of building blocks which are the nodes and edges of the spin network.

Probably my worst moment in science came at a conference in Warsaw when a young physicist named Renate Loll, who had also been a student of Chris Isham in London, announced at the end of her talk that our calculation for the smallest possible volume was wrong. After a lot of argument it turned out that she was right, and we traced our error back to a single sign mistake. But remarkably, our basic pictures and results held up. They have since been confirmed by mathematical physicists who showed that the results we found are underpinned by rigorous mathematical theorems. Their work tells
us that the spin network picture of quantum geometry is not just a product of someone’s imagination - rather, it follows directly from combining the basic principles of quantum theory with those of relativity.

The loop approach to quantum gravity is now a thriving field of research. Many of the older ideas, such as supergravity and the study of quantum black holes, have been incorporated into it. Connections have been discovered to other approaches to quantum gravity, such as Alain Connes’s non-commutative approach to geometry, Roger Penrose’s twistor theory and string theory.

One lesson we have learned from this experience is the extent to which science progresses quickly when people with different backgrounds and educations join forces to push back the frontiers. The relationship between theoretical physicists and mathematical physicists is not always smooth. It is rather like the relationship between the scouts who first explore the frontier, and the farmers who come after them and fence the land and make it productive. The mathematical farmers need to tie everything down, and determine the exact boundaries of an idea or a result, while we physicist scouts like our ideas when they are still a bit wild and untamed. Each has a tendency to think that they did the essential part of the work. But something we and the string theorists have both learned is that in spite of their different ways of working and thinking, it is essential that mathematicians and physicists learn to communicate and work with one another. As happened with general relativity, quantum gravity requires new mathematics as much as it requires new concepts, ideas and ways of doing calculations. If we have made real progress it is because we have discovered that people can work together to invent something that no one person could have come up with alone.

In the end, what is most satisfying about the picture of space given by loop quantum gravity is that it is completely relational. The spin networks do not live in space; their structure generates space. And they are nothing but a structure of relations, governed by how the edges are tied together at the nodes. Also coded in are rules about how the edges may knot and link with one another. It is also very
satisfying that there is a complete correspondence between the classical and quantum pictures of geometry. In classical geometry the volumes of regions and the areas of the surfaces depend on the values of gravitational fields. They are coded in certain complicated collections of mathematical functions, known collectively as the metric tensor. On the other hand, in the quantum picture the geometry is coded in the choice of a spin network. These spin networks correspond to the classical description in that, given any classical geometry, one can find a spin network which describes, to some level of approximation, the same geometry (
Figure 27
).

In classical general relativity the geometry of space evolves in time. For example, when a gravitational wave passes a surface, the area of that surface will oscillate in time. There is an equivalent quantum picture in which the structures of the spin networks may evolve in time in response to the passage of a gravitational wave.
Figure 28
shows some of the simple steps by which a spin network evolves in time. If we let a spin network evolve, we get a discrete spacetime structure. The events of this discrete spacetime are the processes by which changes of the form shown in
Figure 28
occur. We can draw pictures of evolving spin networks; they look like
Figures 29
to
31
. An evolving spin network is very like a spacetime, but it is discrete rather than continuous. We can say what the causal relations are among the events, so it has light cones. But it also has more, for we can draw slices through it that correspond to moments of time. As in relativity theory, there are many different ways of slicing an evolving spin network, so as to see it as a succession of states evolving in time. Thus, the picture of spacetime given by loop quantum gravity agrees with the fundamental principle that in the theory of relativity there are no things, only processes.

John Wheeler used to say that on the Planck scale spacetime would no longer be smooth, but would resemble a foam, which he called spacetime foam. In tribute to Wheeler, the mathematician John Baez has suggested that evolving spin networks be called spin foam. The study of spin foam has sprung up since the mid-1990s. There are several different versions presently under study, invented by Mike Reisenberger, by Louis Crane
and John Barrett, and by Fotini Markopoulou-Kalamara. Carlo Rovelli, John Baez, Renate Loll and many of the other people who contributed to loop quantum gravity are now engaged in the study of spin foam. So this is presently a very lively area of research.
Figure 32
shows a computer simulation of a world with one space and one time dimension, modelled upon ideas from spin foam theory. This is work of Jan Ambjørn, Kostas Anagnastopoulos and Renate Loll. These universes are very small, each edge corresponding to one Planck length. They do not always evolve smoothly; instead, from time to time the size of the universe jumps suddenly. These are the quantum fluctuations of the geometry. After many years, we have here a real quantum theory of the geometry of spacetime.

Simple stages by which a spin network can evolve in time. Each one is a quantum transition of the geometry of space. These are the quantum theoretic analogues of the Einstein equations. [From F. Markopoulou, ‘Dual formulation of spin network evolution’, gr-qc/9704013. All the papers referenced here as gr-qc/xxxx are available at
xxx.lanl.gov
.]

Two pictures of quantum spacetimes. Each event in the quantum spacetime is a simple change in the quantum geometry of space, corresponding to one of the moves shown in
Figure 28
. According to loop quantum gravity, this is what spacetime looks like if we examine it on a time scale of 10
^-43
of a second and a length scale of 10
^-33
of a centimetre. The upper picture shows a single elementary move. The lower one shows a combination of two elementary moves. [From C. Rovelli, ‘The projector on physical states in loop quantum gravity’, gr-qc/9806121.]

Another of the elementary moves for quantum transitions among spin networks, together with the spacetime picture that represents it. [From R. de Pietri, ‘Canonical loop quantum gravity and spin foam models’, gr-qc/ 9903076.]

Is the theory right? We do not know yet. In the end, it will be decided by experiments designed to test the predictions the theory makes about the discreteness of area and volume and other measures of spacetime geometry. I do want to emphasize that although it follows directly from the combination of the principles of general relativity and quantum theory, loop quantum gravity does not need to be the complete story to be true. In particular, the main predictions of the theory, such as the quantization of area and volume, do not depend on many details being correct, only on the most general assumptions drawn from quantum theory and relativity. The predictions do not constrain what else there can be in the world, how many dimensions there are or what the fundamental symmetries are. In particular, they are completely consistent with the basic features of string theory, including the existence of extra dimensions and supersymmetry. I know of no reason to doubt their truth.

Of course, in the end experiment must decide. But can we really hope for experimental confirmation of the structure of space on the Planck scale, 20 orders of magnitude smaller than the proton? Until very recently most of us were sceptical about whether we might see such tests in our lifetime. But
now we know we were being too pessimistic. A very imaginative young Italian physicist, Giovanni Amelino-Camelia, has pointed out that there is a way to test the predictions that the geometry of space is discrete on the Planck scale. His method uses the whole universe as an instrument.

Another picture of a quantum spacetime, showing the causal futures of the events where the spin networks change. These are drawn as light cones, as in Chapter 4. [From F. Markopoulou and L. Smolin, ‘The causal evolution of spin networks’, gr-qc/9702025.]