125 Physics Projects for the Evil Genius (40 page)

where
L
is the length of the string (in meters) and
g
is the gravitational acceleration (9.8 m/s
²
).

This shows the dependence on the square root of the string length. Because there is no mass in the equation, the period does not depend on mass. The period also depends on the gravitational acceleration of the Earth, which under normal circumstances is not a variable.

Try this with a pendulum, consisting of a bowling ball attached to a rope. Make sure the point of attachment and the rope can securely handle the weight of the swinging pendulum.

Try this with a playground swing. Is the natural frequency of oscillation what you predict based on the previous equation? What happens if you push with a rhythm consistent with that natural frequency? What happens if you push with a rhythm very different from the natural frequency?

The period of a pendulum depends on only one variable, which is its length.

A mass hanging from a spring is another example of a system that moves in a repeatable and consistent way. This is called simple harmonic motion. This experiment is about finding what causes a spring pendulum to vibrate faster or slower.

• several masses that can be attached to a string (such as 20 g, 50 g, 100 g, 200 g)
  
• several springs of varying stiffness—it should be possible to
  partially
  stretch the spring by hanging each of the masses to the bottom of the spring. If the masses can’t stretch the spring or if the spring is fully extended while supporting the mass, choose either other masses or other springs
  
• support for each pendulum
  
• stopwatch
  
• meterstick
  
• spring balance (for the extension)
  

1. Set up a spring pendulum consisting of a spring with one end supporting a mass and the other attached to a support above the spring.
   
2. Allow the weight of the mass to stretch the spring and come to rest.
   
3. Pull the pendulum straight
   down
   through a small displacement. (Increasing the elongation of the spring by about 10 percent is a good starting point.)
   
4. Release the pendulum and start the stopwatch as the pendulum is released. Try to release the spring, so it goes up and down in a vertical direction. Bear in mind that, after a few cycles, a spring may have a tendency to start swinging, which complicates the type of motion we are investigating here.
   
5. Count ten cycles up and down. Cycle number one is when the pendulum returns to its original position. Be careful not to count “one” when the pendulum is released.
   
6. Record the time (in seconds) for the pendulum to complete ten complete cycles.
   
7. Divide the time for ten cycles by ten to get the time for one cycle. This is the period of the pendulum for the conditions you are testing.
   
8. As with the previous study, you can approach this investigation in several ways. You are encouraged to develop your own approach to this. Here are a few suggestions:
   

– What variable matters: Mass? Spring stiffness? Amount of displacement? Test the selected variable, while holding the others constant. For instance, you can test squooshy, medium, and stiff springs, all using the same mass and displacement. (We define “squooshy” in quantitative terms in a minute.) Similarly, you can test light, medium, and heavy mass to determine whether the period of the pendulum is dependent on mass.

Figure 67-1 Spring pendulum
.

– Once you determine which variable(s) affects how fast the pendulum swings, you can set up an experiment to measure how the period changes over a range of the variable you selected. The other variables should be kept constant.

The behavior of the spring pendulum is quite different than the swinging (simple) pendulum studied in the previous project.

Two variables are important for a spring pendulum:
mass
and
spring stiffness
.

The heavier the mass, the longer the period. Also, the stiffer the spring, the shorter the period. The “springiness” of a spring is called the
spring constant
, which gives a numeric measure of how stiff a spring is.

Within a fairly broad range, it should not matter whether you pull the spring through a small displacement or a larger displacement.

The dependence of period on mass and spring constant is not linear.

The equation for the period of a spring pendulum (in seconds) is given by:

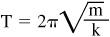
where
m
is the mass (in kilograms) and
k
is the spring constant (in N/m). Notice the period varies as the square root of the mass and the inverse square root of the spring constant.

Predict and measure the period of the spring pendulum. You can do this by first finding the spring constant using the method of
Project 30
. You find the spring constant, k, by measuring the displacement,
x
, of a spring (in m) resulting from a given force,
F
(in N), according to the equation:

k = –F/x

The negative sign reflects the fact that force and displacement are always in the
opposite direction
resulting in a
positive
value for
k
.

Once you have determined the spring constant, predict the period of the spring pendulum using:

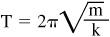
(The period will be given in seconds if the force is entered in
newtons
and the displacement in meters to get k. The mass must be in kg. Remember 1000g = 1kg.) Once you’ve called your shots, set your pendulum in motion and compare your prediction with your measured result.

The period of a spring pendulum increases as the square root of the mass. The period of a spring pendulum increases inversely with the square root of the spring constant.

The simplicity of the spring pendulum provides an excellent opportunity to observe its motion in detail. The movement, like other vibrations in nature, follows a sine wave. We can also identify particular points in the spring’s movement, such as where the velocity is at a maximum and a minimum during its cycle. We can also monitor how the force varies and how it relates to the acceleration. These relationships form the basis for a more complete understanding of how the various aspects of motion are interrelated.

• spring pendulum—set up as in previous experiments
  

1. Set the pendulum in motion and first observe when the following occurs in the cycle:

– Zero velocity

– Maximum velocity

– Zero force

– Maximum force

– Zero acceleration

– Maximum acceleration

2. Place a motion sensor to view the motion of the spring pendulum from underneath. If the mass presents a small target, you can tape an index card to the bottom of the mass to make it easier for the motion sensor to find. (To avoid air resistance, keep it small.)

3. Adjust the settings in the DataStudio program to give the maximum number of readings per second.

4. Open files to read simultaneously: distance, velocity, and acceleration.

5. Displace the spring and be ready to release it.

6. Press Start on the DataStudio screen to begin logging data.

7. Release the spring.

8. Record a few cycles.

9. Adjust the scales, if necessary, to best display the charts. Use the smoothing tools, if needed, to give a smoother curve if the acceleration data appears slightly choppy.

The equilibrium position is the point where the stationary mass hangs without moving. At the equilibrium position, the velocity is maximum, but the force (and, therefore, the acceleration) is zero.

At the maximum displacement position (the point from where the spring was released), the velocity is zero and the force (and, therefore, the acceleration) is maximum. Graphs generated by a motion sensor measuring a pendulum are shown in
Figure 68-1
.

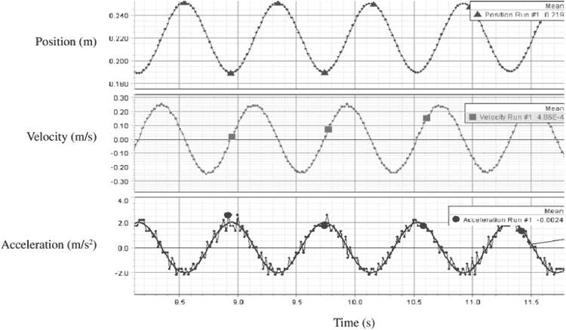
Figure 68-1
DataStudio graphs of motion sensor data showing distance, velocity, and acceleration versus time (setup by T. Dragoiu and J. Silver
).

The distance versus time graph is a sine wave.

The velocity versus time graph is a cosine wave. The velocity is zero when the distance is at a maximum. The two waves have a similar shape, but the velocity curve is delayed by one-quarter of a period compared to the distance curve.

The acceleration curve is also a sine wave. It is at a minimum when the distance is maximum. The acceleration curve is zero when the distance curve is zero. The distance and acceleration curves have a similar shape, except the acceleration curve is delayed by one-half of a wavelength.

A pendulum works because the further the mass moves from equilibrium, the greater the force that returns it to equilibrium. This is the basis of any uniformly vibrating object (known as a
simple harmonic oscillator
). The response of a restoring force, such as exerted by a spring, is to produce motion that follows a sine wave. The acceleration moves in the opposite direction as the distance because the force exerted by a spring is opposite its displacement from equilibrium. This also causes the velocity and acceleration curves to be out of phase with respect to the distance.