125 Physics Projects for the Evil Genius (60 page)

When a conductor is heated, the molecules move in place more rapidly. Like a car moving on a highway with increasing traffic, the electrons cannot move as freely through the conductor. The result is the resistance increases.

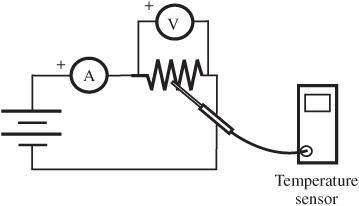
Figure 101-1
Circuit for measuring the effect of heat of resistance
.

Figure 101-2
Resistance versus temperature for 5 cm length of 20 AWG copper
.

Use an external source of heat, such as a hotplate or a Bunsen burner, to heat the (uninsulated) wire.

Use ice, dry ice, or liquid nitrogen to produce low temperatures. Your thermocouple may not read over the entire temperature range of your sample, but you can still obtain some extremely low-temperature readings as the sample warms.

Electrical resistance increases with temperature. This relationship is linear over a broad range of temperatures.

Yes, if the wire is longer or thicker. Copper is well known as a good conductor of electricity. This same is not usually said about iron. This project deals with two ideas that sound similar, but that are quite different: resistance and resistivity.

• uninsulated copper wire 25 cm in length
  
• uninsulated iron wire 25 cm in length of the same diameter (this can be indicated by the wire gauge or AWG)
  
• (other material combinations, such as aluminum or silver wire can be used instead of, or in addition to, copper and iron)
  
• DC power supply
  
• ammeter
  
• voltmeter
  
• (if you have a digital multimeter, you may be able to use the ohmmeter setting directly)
  
• connecting wire
  
• ruler
  

1. Set up the circuit as shown in
   Figure 102-1
   . Mark the wire with a Sharpie in 2 cm (or other convenient) lengths.
   
2. The ammeter is attached across the entire length of the wire. The current from the power supply flows through the entire length of the wire. The voltmeter is attached only across the selected length (2 cm, 4 cm and so on).
   
3. Read voltage, current, and distance.
   
4. Find the electrical resistance from Ohm’s law by dividing the voltage (volts) by the current (amps). This gives a resistance reading in ohms. This can also be directly read from an ohmmeter if you have one.
   
5. Compare the resistance you measure for different lengths.
   
6. For a given diameter, multiplying the resistance by the length gives a measure of the wire’s resistivity. What do you find happens to this value as the length increases?
   

The longer the wire, the greater the resistance.

The greater the cross-sectional area of the wire, the lower the resistance.

Resistance increases (linearly) with length.

Resistance is inversely proportional to cross-sectional area. This is represented in
Figure 102-2
.

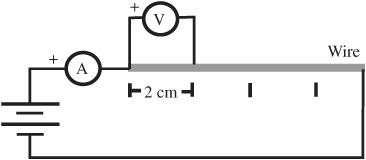
Figure 102-1
Circuit for measuring resistivity
.

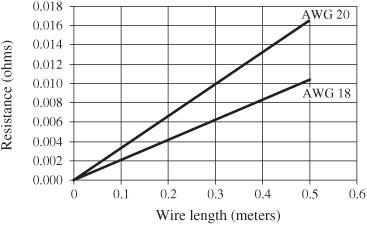
Figure 102-2
Resistance of various lengths of copper wire
.

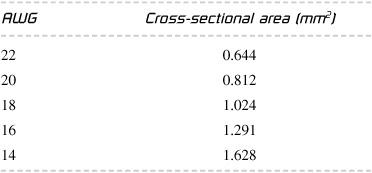
The cross-sectional areas of the various American wire gauges (AWG) are shown in
Table 102-1
.

Table 102-1

Resistivity at 20 degrees C for various materials used to make wires is shown in
Table 102-2
. This tells how much resistance is contributed by every meter of wire.

Table 102-2

For a given wire size, resistance is proportional to the material’s resistivity, according to the equation:

R = ρL/A

where
R
is resistance in ohms

ρ is the resistivity in ohm-cm (ρ is the Greek letter “rho”)

L
is length in centimeters

A
is cross-sectional area in centimeters.

A less precise, but possibly more fun, approach to this experiment is to use wires cut from food items, such as pickles or fruit, or by forming wires from Play Dough.

The wire can be sliced in sections as it is measured to shorten its length. This approach may require the use of two meters because the ohmmeter may not be stable.

This can be taken a step further by comparing the
resistance
to the
resistivity
. You can get the resistivity by multiplying the resistance by the length of the wire (in cm) and the area of the wire (in cm
²
). You can get the area of the wire from using a measured or looked-up value for the wire diameter and using the equation:

A = πr
²

where
r
is the radius of the wire.

Resistance
is a measure of how difficult it is for a given voltage to force electrons through a conductor. It doesn’t matter how big or small the piece of conductor. All that matters is the overall effect it has in the electrical circuit.

On the other hand,
resistivity
is a measure of how effective a particular material is in impeding the flow of electrons. Resistivity is the same for any particular material.

Resistance combines the effect of the material’s resistivity, as well as its length and cross-section.

A
capacitor
is an electronic component that can store an electrical charge. Unlike a battery that stores electrical charge through chemical reactions, the capacitor holds electrons on conductive plates separated by an insulator. Capacitors are present in numerous electronic circuits. They are also gaining attention recently as a possible means of supplementing batteries in electric cars. This experiment explores how capacitors can be charged and discharged.

• 1000 μF (micro-Farad) capacitor
  
• 50 kΩ (kilo-Ohm) resistor (note other capacitor/resistor combinations that can work are listed in
  Table 103-1
  )
  
• DC voltmeter (or multimeter configured as a voltmeter)
  
• 10-volt DC power supply
  
• DC ammeter (with 0–1.0 mA range)
  
• 3 knife switches (SW1, SW2, and SW3)
  
• jumper wire
  
• stopwatch
  
• 2 LEDs
  

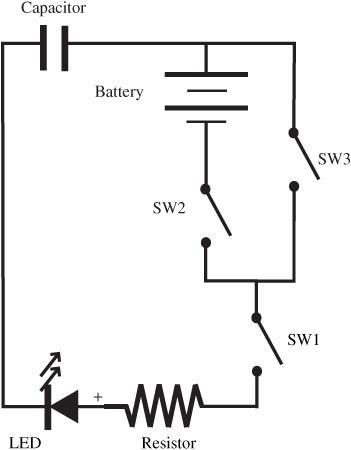
1. Set up the circuit shown in
Figure 103-1
. Pay attention to the positive and negative polarity markings, especially if your capacitor has a designated positive side (some do and some don’t). Start with all switches open.

2. Close SW2. Leave open SW3.

3. Close SW1 and start the timer.