Beyond the God Particle (22 page)
Read Beyond the God Particle Online
Authors: Leon M. Lederman,Christopher T. Hill
Tags: #Science, #Cosmology, #History, #Physics, #Nuclear, #General

It also turns out that the gauge symmetry principle is intimately related to quantum theory. Without the quantum waves that describe electrons and other charged particles, together with photons, the gauge symmetry seems awkward—there's no electron wave to “transform” under the gauge
symmetry—there's no “representation” of the gauge transformation, like the wine bottle that rotates when we do a rotation transformation in space. It was as if electromagnetic theory, created by wizards in the nineteenth century, was waiting and begging for the quantum theory to come along and make it whole. And, if you try to modify electromagnetism to make the gauge fields directly observable, the whole structure of the quantum theory breaks down and becomes a heap of rubble. The key to cloaking the gauge field—making it unobservable while the derived magnetic and electric fields are observable—is the conservation of electric charge. But now we encounter the weak interactions with the three new gauge bosons, W
+
W
–
and Z
0
and all particles now have weak charges. Again, as in electromagnetism, we find that the weak charge, like the electric charge, must also be conserved.
The weak charge of the L muon is –1 (in some units). But the parity violations experiment tells us that
the weak charge of the R muon is zero.
L particles have weak charge while R particles do not
. So now the marching L-R-L-R-L of a massive muon (or electron or top quark—any other matter particle will do) creates a problem. As L turns into R, the weak charge of the muon changes from –1 to 0.
The weak charge is evidently not conserved for a massive muon sitting at rest, minding its own business, and oscillating between L and R.
Mass breaks the vaulted gauge symmetry, which we have now extended to include the W
+
, W
–
, and Z
0
bosons. But without conserved charge,
the gauge theory collapses into charred remains
.
Please reread the previous paragraph. This is what directly leads us to the Higgs boson.
The original paper of Sheldon Glashow on the Standard Model of electromagnetic and weak interactions defined the basic structure of the weak and electromagnetic gauge symmetries and introduced the W
+
, W
–
, Z
0
.
5
However, Glashow needed masses to explain the physical world, so he “put them in by hand,” knowing this was a serious problem but thinking a solution would come later. This, therefore, was not yet a mathematically complete theory, and it wasn't understood if it could ever be made compatible with the principles of quantum mechanics at the time.
In 1967 Steven Weinberg wrote what has become an iconic paper of the Standard Model, “A Model of Leptons.”
6
He took Glashow's theory and proposed a clever remedy to the problem of mass, focusing only on
the electron and its neutrino. He was inspired by the paper of Peter Higgs, but had to refine Higgs's idea to make it work. In the end, Weinberg had engineered a kind of “superconductor” that made the W
+
, W
–
, and Z
0
bosons heavy, while the photon remained massless. He also showed how the masses of all the matter particles, electrons, muons, the top quark, even ultimately neutrinos, could be explained. Without Weinberg's idea it would not be possible to have a consistent theory of mass for any of the elementary particles.
Even after Weinberg launched his paper, many people had reservations about whether the theory really was truly mathematically consistent, and the idea didn't catch on immediately. It took the super heroic efforts of Gerard ‘t Hooft and Martinus Veltman to show that it was indeed a workable and useful theory, and to show us how to use it correctly.
7
This opened a scientific discovery floodgate, and the “gauge theory revolution” began. A number of key refinements and major extensions were required to accommodate the quarks and the strong interactions. The rest was up to the theorists to compute the various predictions for physical processes, and to the experimentalists to measure these things and test the theory. It has proved to be a stunning success.
ENTER THE HIGGS BOSON
Recall that our problem is to make a massive muon march, oscillating L-R-L-R-L-R, even though each time L changes to R the weak charge changes from –1 to 0. How do we do it? As the muon simply sits at rest it is rapidly “oscillating” L-R-L-R…its weak charge is also oscillating: –1 0 –1 0…. The weak charge is flickering on-off-on-off. The mass of the muon seems to destroy the neat conservation law of the weak charge. The Standard Model must either be wrong—or something new is happening to rescue it.
Graham: “So, let me ask a simpler question: Is there any way, or any process, even if it's only theoretical gibberish, in which an L muon can convert to an R muon and still conserve the weak charge?”
In fact…yes! There is…and this is the key! If we introduce a new kind of boson
that has the same weak charge as the L muon
, a boson that also has weak charge –1, then the L muon could “convert” to such a boson, plus
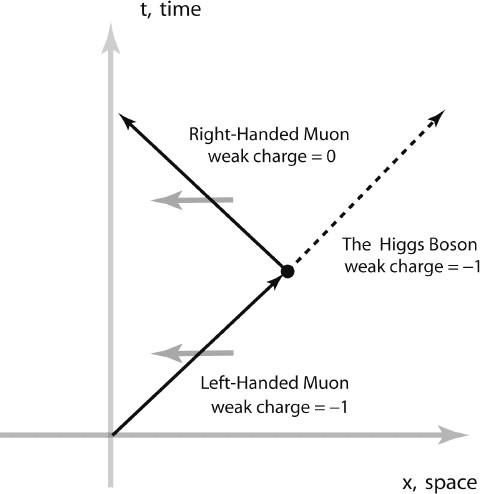
an R muon. When the initial L muon has weak charge –1 and converts to the R muon with weak charge 0, plus the new boson that has weak charge –1, the overall weak charge remains the same since –1 = 0 + (–1). The required space-time picture is shown in
figure 6.22
.
Figure 6.22. Muon Coupled to Higgs Boson.
An incoming L muon with weak charge -1 converts to a recoil R muon with weak charge 0, plus the Higgs boson with weak charge -1 and spin 0. The process has a “coupling strength” g
µ
. It unites the L muon with the R muon. The Higgs boson must carry a weak charge equal to that of the L muon, so the weak charge is conserved. The Higgs boson must also have spin 0 to conserve spin angular momentum.
The properties of our new boson are completely dictated by this process (this is explained in detail in the caption of
figure 6.22
). Since the L muon is converting to an R muon, maintaining a constant spin direction, the new boson must have zero spin. Note that since the L muon and R muon have the same electric charge, –1, the new boson must therefore have zero electric charge. And the key to the whole game, since the incoming L muon has weak charge –1 and the outgoing R muon has weak charge 0 is that the new boson must have weak charge –1. Voilà! We have completely spelled out the properties of the new boson. We have done exactly what Weinberg did in his 1967 paper. We have introduced a new theoretical particle, a spin-0 boson, that carries weak charge. We call this the Higgs boson.
BUT WHAT ABOUT MASS?
We're almost there. I can just taste those rainbow trout that we'll soon be catching at the mountain lake once we put our fishing gear into action. It's just another 50 feet…take a deep breath. The grandest peak of all will soon come into view.
What do we mean by “boson”? For reasons that are deep and profound and have to do with quantum fields and relativity, there is a remarkable difference between matter fields, like electrons and muons and quarks, etc., and things we call the force carriers, the “bosons.” Matter particles are called “fermions” after Enrico Fermi. For no reason connected to their namesake, they are recluses and like to keep away from other fermions (Fermi was quite outgoing and personable).
Fermions like to avoid one another. We can never get two fermions into the same quantum state—they are forbidden from doing this. This is a deep principle and has to do with the weird quantum attribute of spin.
8
This property was discovered in the process of understanding atoms, and without it there would be no chemistry—all atoms would collapse down into different forms of the chemically inert helium—the universe would forever be one big gas bag of non-interacting helium-like atoms.
Bosons are named after the Indian physicist Satyendra Nath Bose, who was a friend of Einstein.
9
Bosons are gregarious particles (unlike their namesake, who was kind of shy). Bosons love hot tubs. They all pile into the same
quantum state together whenever they can. In fact, whenever bosons start to pile into the same state, one of them yells “Party's on,” and pretty soon a gazillion bosons end up in the same state. You've seen this phenomenon in the dramatic instance of a laser beam, where many photons, which are each bosons, pile into exactly the same state of motion with the exact same frequency and wavelength of light, making a mysterious and intense beam of light.
But there's a more mundane example. Any old electric or magnetic field is just a very large and indefinite number of photons dancing around in a small set of quantum states. This is called a “classical coherent state.” The quantum particle aspect of this becomes so blended that all we see is a large macroscopic wavelike field, and it is described by Maxwell's classical equations of electromagnetism. The blending into a coherent or “collective” state masks the quantum nature of the photons that make up the field. The same is true of the radio waves delivering text messages to your iPhone
®
. These are large aggregates of photons that behave “collectively” like one big field, doing exactly what bosons love to do.
THE HIGGS VACUUM
Weinberg realized that this bosonic “piling on” into one big collective state could also happen to the Higgs boson. We need only create an enormous “Higgs field” that permeates the entire universe. This field is similar to the magnetic field of the earth, in that it is composed of the Higgs bosons acting collectively, while magnetic fields are composed of photons acting collectively. However, magnetic fields have a well-defined direction in space—defined by the direction the compass needle points—we call a magnetic field a “vector field.” The Higgs field, on the other hand, just has a value—measured in energy—it has no direction in space. We call it a “scalar field.”
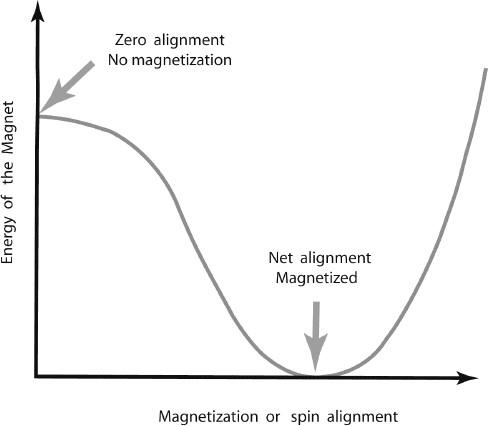
Why would the universe have such a field? There is again a clever idea that the particle theorists borrowed from the study of materials—in this case the phenomenon of ferromagnetism. An iron magnet will spontaneously magnetize when it is cooled. The magnetic field seems to pop out of nowhere, but it is actually coming from the trillions and trillions of atoms inside the iron magnet. Each atom has a spin and is a little magnet itself.
For iron, when it is cooled, these atomic spins all line up and point in the same direction. This creates a large magnetic field.
10
While magnets are complicated in detail, we can understand iron in a simple way through a plot. The point is that the energy of the iron is reduced the more the atoms’ spins are aligned. This comes from the complex interactions of the atoms with each other in the iron material. If we have misaligned atoms, or random atomic spins that have no net alignment, we have a state of higher energy. The state in which all atomic spins are aligned has much less energy, and for some particular amount of alignment, or “magnetization,” we get the lowest energy state. The magnetic field then appears
spontaneously
.
Figure 6.23. Magnetic Potential.
The energy of an iron magnet as function of its magnetization shows that the minimum energy occurs for a nonzero value of the magnetization. This is why magnets form a stable state with a nonzero magnetic field.