Beyond the God Particle (23 page)
Read Beyond the God Particle Online
Authors: Leon M. Lederman,Christopher T. Hill
Tags: #Science, #Cosmology, #History, #Physics, #Nuclear, #General

Figure 6.24. The Higgs Potential.
We can adapt the principle of an iron magnet to the vacuum energy of the Higgs boson. The energy of the vacuum has a minimum for a nonzero value of the Higgs field. This causes the vacuum to develop a nonzero Higgs field everywhere throughout space. The parameters are tuned to produce a Higgs field strength in the vacuum of 175 GeV, the value that is inferred from Fermi's theory of the weak interaction and the muon lifetime.
We use this idea, theoretically, to make our Higgs field fill the vacuum. A vacuum in which the Higgs field is zero is simply “engineered” to be a state that has a higher energy than one in which the Higgs field has a nonzero value. Theorists know immediately how to do this: one simply relabels
figure 6.23
for an iron magnetic, replacing “energy of the magnet” by “energy of the vacuum,” and “magnetization” by “Higgs field.” In this way we get the (now-famous) “Higgs potential” shown in
figure 6.24
. The
preferred value of the Higgs field is just the location on the x-axis of the minimum energy point of the potential. This is the value the Higgs field will have throughout all of space. We can determine what it must be from Fermi's original theory. It is an energy and has a value of about v = 175 GeV. Voilà!
Katherine: “But once we have filled the vacuum with an enormous Higgs field, why can't we just go out in our backyard and pluck a Higgs particle from the vacuum? Why do we need the LHC at CERN?”
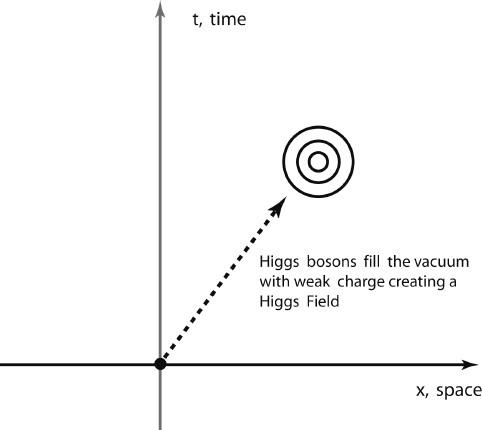
Figure 6.25. Higgs Field Fills the Vacuum.
Higgs bosons form a field in the vacuum, represented by the circles, much like photons can form an electric or magnetic field. The Higgs field contains an indefinite number of bosons and an indefinite weak charge. A Higgs boson particle that undergoes a quantum fluctuation into a state of zero energy and zero momentum can “disappear” into the field (or “appear” from the field). The vacuum becomes a reservoir of weak charge.
Very good question, but it has a simple answer. The photon, which makes large electric and magnetic fields, has zero mass, so it isn't too hard to pluck a photon out of a large electromagnetic field. For example, we can have a source of light, like a laser beam, that is full of photons and that looks very coherent, as though there are no particles there. But we can also spread the beam out and make it very dim and put a “photon counter” or photo-cell hooked up to a computer, and we then see “tick…tick, tick…tick….” as individual photons are counted. We've thus plucked the photon particles out of the laser beam. These are very low-energy particles that can easily be detected by a sensitive detector. In fact, that's exactly what the silver halide crystals in an old photographic emulsion do: they react to individual photons as particles and when developed, give us a pretty picture, like Ansel Adam's view of the Grand Tetons.
And, indeed, the Higgs field that permeates the universe implies that Higgs bosons, as particles, are lurking inside the vacuum. However, the Higgs boson particles that collectively make up the Higgs field are very heavy particles. It takes a big sledgehammer to knock one out of the vacuum, and that's exactly what the LHC is doing.
But there's something else really interesting about the Higgs field—its existence means that the vacuum is full of weak charge. Recall that the Higgs boson must have a weak charge of –1 because it couples to L (–1 weak charge) and R (0 weak charge). The Higgs field throughout space means that the vacuum has become an enormous reservoir full of weak charge. We can borrow weak charge from the vacuum and, in so doing, turn a lowly R muon into an L muon. And an L muon can dump its weak charge into the vacuum and become an R muon. Eureka! We now see how the muon gets its mass by flipping from L-R-L-R. The flip involves a certain “coupling strength” of the muon to the Higgs boson, called g
µ
. The mass of the muon is then determined: it is simply m
µ
= g
µ
(times) 175 GeV.
The problem of giving the masses to the elementary particles is solved! The vacuum is an enormous reservoir of weak charge. R particles that have no weak charge absorb the weak charge from the vacuum to become L particles. L particles that carry weak charge dump their charge into the vacuum to become R particles. Since the great reservoir of weak charge, the Higgs field, fills all space for all time, the masses of the elementary particles are generated throughout all space and time. The gauge symmetry, i.e., the
conservation of weak charge, is still in effect, operating at the microscopic level.
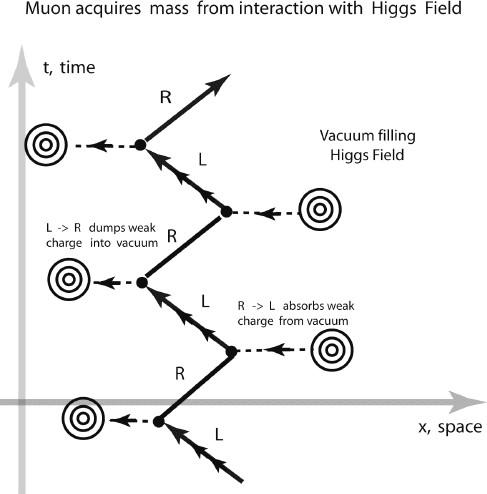
Figure 6.26. Muon Mass from the Higgs Field.
The Higgs field, together with the coupling of the Higgs bosons to all particles, as in
figure 6.22
, gives rise to mass. The L muon can convert to an R muon and radiate a zero-energy Higgs boson that disappears into the field and carries away weak charge. In the figure the multiple arrows show the flow of weak charge out of the vacuum as R converts to L, then back into the vacuum as L converts to R. This also happens for electrons, the other leptons, and the quarks.
Alas, aside from solving the conceptual problem of making mass while preserving gauge symmetry, the formula m
µ
= g
µ
(times) v, where v = 175 GeV/c
2
tells us very little. The problem is that the Standard Model doesn't
predict
the value of g
µ
for us or the coupling of any other fermions to the Higgs boson, for that matter. All we can do is to go out and measure the mass of the muon, m
µ
, and from that we can determine g
µ
= m
µ
/v. The measured mass of the muon is about 0.1 GeV/c
2
, giving g
µ
= m
µ
/v = 0.1/175 = 0.00057. Likewise, the electron has a measured mass of about 0.0005 GeV/c
2
, and therefore the electron couples to the Higgs boson with coupling strength g
e
= 0.0005/175 = 0.0000028. The top quark has a measured mass of about 172 GeV/c
2
, and therefore has a coupling to the Higgs that is nearly 1, i.e., g
t
= 172/175 = 0.98. Here we've simply swapped the unpredicted masses of these particles for the unpredicted coupling strengths to the Higgs boson, g
µ
, g
e
, g
t
, etc. But the Standard Model, through the Higgs boson, also generates the heavy masses of the W
+
, W
–
, and Z
0
bosons. These particles’ masses were predicted by the theory, and the agreement between experiment and theory is spectacular. We leave the job of constructing a more complete theory that predicts the origin and mathematical values of the Higgs coupling constants to a future, younger generation.
We've arrived at the Rainbow Trout Lake, and we've just caught a big one. All particle masses, the L-R-L-R march through space-time, are due to the oscillation of L into R, and each time L turns to R it dumps a unit of weak charge into the vacuum via the Higgs field. And each time an R turns into an L it absorbs weak charge back out of the vacuum.
That is the origin of mass
. So, yes, Katherine, indeed you can “pluck a Higgs out of the vacuum,” but to make and study the Higgs boson particle directly requires the sledgehammer of the CERN LHC. Our entire world is sculpted by the grand Higgs field that surrounds us. It's a little spooky.
LET'S TAKE A BREAK
Breathe in the cool and pure mountain air. We've fast-forwarded through the entire twentieth-century physics to get here. We deserve a break and a few moments to soak in the serene beauty of the mountain peaks and our lovely lake. We've just filled our basket with rainbow trout, and it'll soon be time to start back down the mountain. In fact, we are at the pinnacle. We now understand what the Higgs boson is and how its field fills the entire
universe and how particles undergoing their L-R-L-R march through space-time are absorbing and reemitting weak charge, to and fro, into the vacuum itself. It's happening before us and all around us as we linger. All of the particles that make up our mountain, our lake, our trout, and us, are doing the L-R-L-R march and interacting with the grand Higgs-filled vacuum, dumping and absorbing weak charge as they go. And, on July 4, 2012, the experiments at the CERN LHC, finally confirmed to the entire world that it is true: The Higgs boson, the “particle comprising the Higgs field,” the particles that collectively make up this vast hot tub of a vacuum in the universe in which we live, has finally been seen in the laboratory.

Our neighbors often ask, “So what do you folks do over there at Fermilab?” We would often tell them that “Fermilab has
the world's most powerful microscope
.” This was true until November 20, 2009.
“The LHC is back,” the European Organization for Nuclear Research announced triumphantly Friday, as the world's largest particle accelerator resumed operation more than a year after an electrical failure shut it down.
Restarting the Large Hadron Collider—the $10 billion research tool's full name—has been “a herculean effort,” CERN's director for accelerators, Steve Myers, said in a statement announcing the success. Experiments at the LHC may help answer fundamental questions…which deal with [the particles of] matter far too small to see.
1
The LHC was back after the challenging rebuilding process following its cataclysmic magnet explosion on September 19, 2008 (see
chapter 1
, under the heading “Oh, $%&#!”). At that time, the world's most powerful particle accelerator became the fully operational Large Hadron Collider (LHC) at CERN in Geneva, Switzerland. At that moment, a little-noted passage in history of profound significance had occurred: Europe became home to the world's most powerful microscope after nearly a century of US preeminence. The Fermilab Tevatron was switched off permanently on September 30, 2011. However, just as there are many kinds of microscopes, there are also many kinds of particle accelerators. Even today, Fermilab still operates many of the original onsite accelerators since the Tevatron shut down.
We think that the “the world's most powerful microscope” reply to
our neighbors’ question about the Tevatron then and the LHC now is the simplest and best “sound byte” one can give to the nonexpert—someone who may be curious about particle physics or about whatever mysterious things we do with these large devices. There were never any bombs built at Fermilab or CERN, and no UFOs are buried deep underground at the sites. It is all science, with the
biggest microscopes in the world
. The science of particle physics deploys accelerators, aka powerful microscopes, to study the smallest objects in nature—plain and simple. Our neighbors would usually remark at this point, “Oh! So that's what you do over there—how interesting,” and then they might say something like “Hmm…I always thought it was something else.”