Beyond the God Particle (19 page)

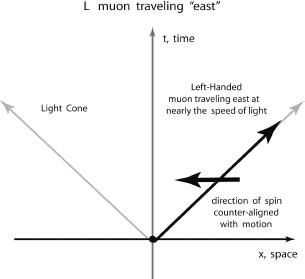
Figures 5.15a–d. Motion of Muon through Space-Time as chiral. Figure 5.15 a.
A right-handed particle has its spin (as defined by the right-hand rule) aligned with the direction of motion. As the particle approaches the speed of light we call this “right-handed chirality.” Here the particle is moving “east” while the spin is also pointed “east.”

Figure 5.15b.
A left-handed particle has its spin (as defined by the right-hand rule) aligned opposite to the direction of motion. As the particle approaches the speed of light we call this “left-handed chirality.” Here the particle is moving “east” while the spin is pointed “west.”

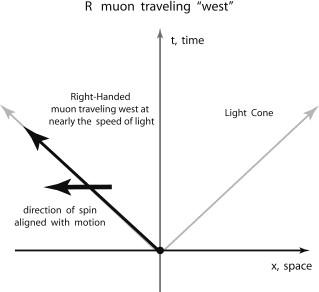
Figure 5.15c.
A right-handed particle has its spin (as defined by the right-hand rule) aligned with the direction of motion. Here the particle is moving “west” while the spin is also pointed “west.”

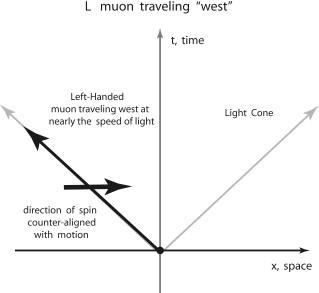
Figure 5.15d.
A left-handed particle has its spin (as defined by the right-hand rule) aligned opposite to the direction of motion. Here the particle is moving “west” while the spin is pointed “east.”

THE FORCES OF NATURE KNOW ABOUT CHIRALITY

The forces of nature respect certain laws that govern everything. Perhaps one of the most important of these is the law of conservation of energy. The total energy of a system before an interaction occurs is the same as the total energy afterward. Likewise, you are probably familiar with the conservation of momentum, which is why it's hard to stop on a slippery surface, and the conservation of angular momentum, by which gyroscopes always like to point in the same direction and by which it is even possible to ride a bicycle or a motorcycle.

Now we learn a new and somewhat obscure conservation law: it is a stunning fact that all known fundamental (gauge) forces among elementary particles in nature share a special property. They also “conserve chirality.”

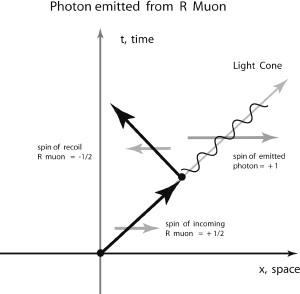
For example, if a photon interacts with an R particle, the particle will remain R (see
figure 5.16a
). A photon cannot convert R particles into L (or vice versa). This means that the R particle is really quite independent of the L particle as far as electromagnetism is concerned (so, too, the strong force of quarks, where we replace the photon by the “gluon,” and likewise for the weak force, which we'll soon discuss in detail). The interaction strength of the force of electromagnetism, i.e., the electric charge, of an R muon is exactly the same as that of an L muon, even though a photon only makes R go to R, and L go to L.

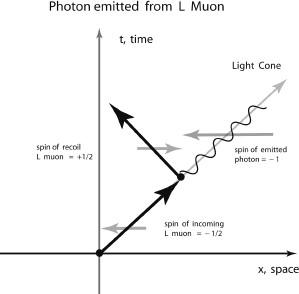
Figure 5.16a.
A photon is emitted from an incoming right-handed chirality muon. The muon recoils (changes direction) and its spin simultaneously flips, so that the outgoing muon is also right-handed chirality. Note that the initial spin is +1/2. The emitted photon has spin +1, and the outoing muon has spin –1/2, so the total spin angular momentum is conserved since +1/2 = +1 + (–1/2).

Figure 5.16b.
A photon is emitted from an incoming left-handed chirality muon. The muon recoils and its spin flips, so that the outgoing muon is also left-handed chirality. Note that the initial spin is –1/2. The emitted photon has spin -1, and the outoing muon now has spin +1/2, so the total spin angular momentum is conserved since: –1/2 = –1 + 1/2.

RESTORING MASS TO THE MUON

Now let's turn the muon mass back on. Of course, our muon always had a mass, but we made its effects unnoticeable by accelerating the muon up to the speed of light. Mass permits a particle, such as our muon, to travel at any speeds less than c, or to sit still at rest.

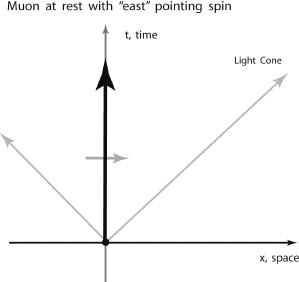
Figure 5.17.
A muon at rest has a spin that points in the space direction, but it has no spatial velocity. Therefore, it has no definite chirality. The chirality is meaningful as a symmetry only when the muon is massless, travels at the speed of light, whence the R and L muons become distinct particles. Chirality then becomes conserved.

In
figure 5.17
we see a massive muon at rest. It simply moves forward through time, with no progression through space. It has spin, but it has no chirality, because there's no direction in space of velocity to compare the spin direction to. Somehow our two independent chiral states of the muon, L and R, must still be there, but they are now blended together to make a resting muon. How?

Nature does this trick by the effect of mass. But mass in particle physics has a new meaning.
Mass makes an L chiral particle oscillate into a R chiral particle and back again
, without changing the direction of the spin (recall that spin is conserved, the conservation of angular momentum, and the resting muon isn't interacting with anything that can flip the spin around). Mass changes chirality from L to R or vice versa.

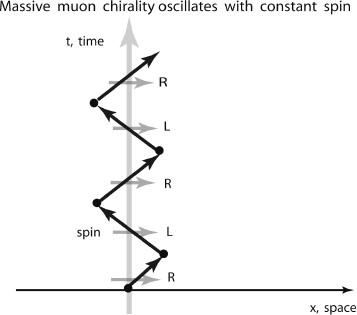
Figure 5.18.
At the quantum level, a muon at rest has a definite spin, but it is oscillating rapidly between L and R chirality.

So, the resulting motion of the resting or slow, massive muon, in terms of its two chiral parts, is actually a kind of forced march. The muon goes R-L-R-L-R…, to the grunting call of the drill sergeant, called “mass,” even though it is sitting still, simply moving forward in time. Each time the muon oscillates, it flips from being an R muon to an L muon back to an R muon again, over and over. The chirality
is not conserved
, that is, it is not always the same for particles that have mass. L and R are blended into one marching particle that hobbles through space and time oscillating between its schizophrenic parts of left- and right-handed chirality.

In this R-L-R-L oscillation the direction of the spin stays the same (the spin is “conserved”), and the electric charge remains the same since L and R muons both have the same electric charges. The R muon and L muon oscillate back and forth between one another, so on average the muon can sit still in space, or move along very slowly with a definite value of its spin in the eastward direction. We have a name for this rapid oscillation of the muon between its two chiralites: we call it “Zitterbewegung.”
⁵

So the ancient concept of mass is now seen to be richer in the fundamental world of the elementary particles out of which we are built. It now
involves “zitter”—the rapid oscillation between L and R. As the muon approaches the speed of light, time becomes frozen, and the muon becomes frozen into either an independent L or R state.

But now let's reconsider the conservation of electric charge. The chirality was conserved by the interaction of the muon with the photon, even though chirality flips L-R-L-R…due to mass. But this means that we can make a massive muon (or a massive electron, or a massive proton, or massive quarks inside the proton) out of two different pieces, L and R,
only if the two pieces have the same electric charge
. Electric charge cannot be created out of nothing or made to vanish into nothing. That is,
electric charge must be conserved in nature
: this is a fundamental law of nature.